I have a $6\times 12 $ rectangle, which I need to fill by the following figure:
What is the minimum number of figures I need to use, so that no additional figure can be added? The figure can be rotated but cannot overlap.
How this question can be solved mathematically without trial and error:
Here is one possible answer:
You want to compute the independent domination number of a graph with one node per tromino and an edge for each pair of trominoes that overlap. You can solve the problem via integer linear programming, as shown in my answer here. Optimal values for $n \times 2n$ with $n\in\{1,\dots,10\}$ are $0, 2, 3, 6, 9, \color{red}{12}, 17, 22, 28, 35$.
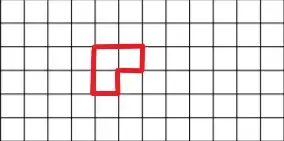
This answer just establishes a lower bound of $11$ tiles. Perhaps the idea can be pushed further to get to $12$.
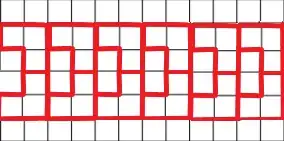
The number of $2\times2$-squares in the $6\times12$-rectangle is precisely $5\times11=55$, and every such $2\times2$-squares allows for $4$ ways to place the figure in it. So there are $4\times55=220$ ways to place the figure in the rectangle.
With every figure we place, we exclude a number of other placements of the figure:
So to exclude all $220$ placements we certainly need at least $\lceil\tfrac{220}{27}\rceil=9$ figures. This is of course a weak lower bound; there is no such ideal placement of $9$ figures that excludes all other placements. For starters, note that to exclude the four corner placements, in wich a figure covers one corner square and the two adjacent edge squares, we must place a figure along an edge or in a corner. This shows that we need at least $4$ edge or corner placements. Together these exclude at most $4\times21=84$ placements, and so to exclude the remaining $220-84=136$ placements we need at least $\lceil\tfrac{136}{27}\rceil=6$ tiles. So we need at least $4+6=10$ figures.
We can improve this bound further: For every interior placement of a figure, the $12$ squares that are directly adjacent (including diagonally) allow for $6$ ways to place a figure entirely inside the adjacent squares:
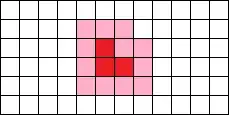
To exclude these $6$ placements we must place figures in such a way that they exclude some placements already excluded by the original placement, shown in red. It is not hard to verify that in this way, at least $10$ placements excluded by the red placement will also be excluded by another placement. That is to say, for every interior placement there will be $10$ out of $27$ placements that will be excluded twice. So effectively an interior placement excludes at most $27-\tfrac{10}{2}=22$ placements. So we need at least $4+\lceil\tfrac{136}{22}\rceil=11$ figures.
