There is a neat naming scheme for pentominoes based on letters they resemble. Is there a generalized naming scheme for polyominoes? If there isn't a canonical one, can you think of a good one?
Criteria
No takers yet, so I'll give it a shot. Roughly, we can use some of the same strategies as naming carbon chains in organic chemistry: labeling long chains and then adding branches.
The simplest polyominoes are those with $n$ blocks in a straight line. We call the $n$th straight line polyomino $_nA$. For convenience later, we will construct $_nA$ from a preferred end by adding one block at a time. The polyominos $_1A$ through $_5A$ are below:
For polyominoes which are straight but for a single bend, we start from the end closest to the bend, and mark the block where the first bend occurs as a superscript or subscript if it is a left or right bend respectively. If we don't allow reflections, then $_4A^2$ and $_4A_2$ are distinct. We would never write $_4A^3$, for example because that wouldn't have started counting from the end closest to the bend.
If there are multiple bends, we include the locations of all bends and directions:
We can establish conventions like preferring smaller sets of indeces of bends, and preferring to start with a right turn. These are demonstrated above: we choose $_5A_{2,4}^3$ rather than $_5A_{3}^{2,4}$ because the right turn comes first in the former.
If the polyomino has branches, we can start with the longest branch and "sum" on the branches. The sum $+_n$ attaches the second term to the first at the $n$th side starting from the first. We can use parentheses to attach multiple branches.
Using this notation, we can describe every polyomino. However, we might want to add other elements like $m\times n$ blocks $_{mn}B_m$:
The preferred side for numbering will be the far left of the bottom when the block is oriented vertically. We can add any number of strings to a block, and we will always start with the biggest block.
In principle, we can attach more blocks or chains on the end of any branch. If we wanted to make further simplifications, we could define rings by the polyominos they surround:
Of course, with every simplification we make, we need to add more constraints so that we choose unique names for each polyomino. However, this description shows that in principle we can find a naming scheme for all polyominos.
Here are the named pentominoes. This scheme has the property that unbranched chiral pentominoes are obtained from their mirror images by switching subscripts and superscripts.
Oh, this looks like fun! Allow me to run with orlandpm's notation scheme by proposing a corresponding (natural language) naming scheme.
The simplest polyominoes $_1A,_2A,_3A,_4A,_5A,_6A,_7A,_8A,_9A,_{10}A,_{11}A,_{12}A,_{13}A,\dots$ we call henpo, dipo, tripo, tetrapo, pentapo, hexapo, heptapo, octapo, enneapo, decapo, hendecapo, dodecapo, triskaidecapo, and so on. Here we combine a Greek numeral prefix with "po", taken from the Greek "potami" meaning river (and nicely dovetailing with the word "polyomino").
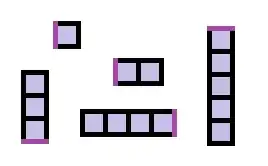
For polyominoes which are straight but for a single bend, such as $_4A^2$ and $_4A_2$, we append a numeral prefix and either "ar" (for a left turn) or "dex" for a right turn. The three tetrominoes below would be named tetrapo, tetrapodiar, and tetrapodidex. (Collapse two consecutive "a"s to one, so that $_8A_4$ would be octapotetrar rather than "octapotetraar".)
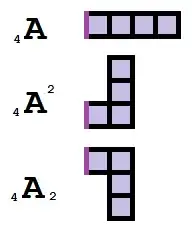
If there are multiple bends, we keep appending. The first polyomino below can be called "pentapodidextriartetradex". I propose that if a turn occurs directly after a previous turn, then the numeral prefix can be omitted. Thus the first polyomino below would preferably be called pentapodidexardex. Similarly, the second polyomino is called octapodiardexardexheptadex.
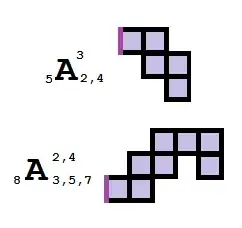
If the polyomino has branches, we concatenate the names of the subpolyominos, with two additional changes. First indicate what base polyomino we are attaching subsidiary polyominoes to by changing the base's "po" to its long-form "pota". Second, we indicate the location of the attachment with a numeral prefix and "sy" (from "synapto", attach). The first polyomino below is dodecapopentarheptar, while the second one is dodecapotapentarheptartetrasydipo.
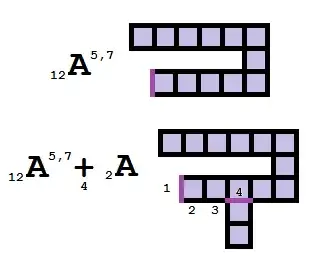
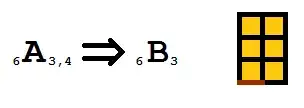
For blocks $_{mn}B_m$, we use the area's numeral prefix followed by "lim" (from "limni", lake), then the height's numeral prefix followed by "ups" ("upsos", height). (Some might have preferred "yps". We replace "au" by "u".) For example, a $4\times3$ block would be dodecalimtetrups, while a $6\times2$ block would be dodecalimhexups. For numbers with only one nontrivial factorization (that is, products of two primes or squares or cubes of primes), the height and "ups" should be omitted: the $_6B_3$ below is called hexalim rather than "hexalimtriups". (Its river-form name $_6A_{3,4}$ would have been "hexapotridexdex".) If a block is the base polyomino for attachments, we change "lim" to the long-form "limni".
The first two polyominoes below are hexalimnitetrasytetrapo and hexalimnitetrasytetrapohexasytripodiar. I think the third one should be ${}_6B_3 ( {}\mathop{+}_4 {}_4A\ ( {}\mathop{+}_9 {}_1A \ ) )$ rather than ${}_6B_3 ( {}\mathop{+}_4 {}_4A\ ( {}\mathop{+}_2 {}_1A \ ) )$; hence its name would be "hexalimnitetrasytetrapotaenneasyhenpo". If a single block is the polyomino being attached, the "henpo" should be omitted, so that the third polyomino below is simply hexalimnitetrasytetrapotaenneasy.
Note a difference between the second and third names: in the second name, we had the long form "limni" but the short form "po", indicating that both subsidiary polyominoes are attached to the first one. In the third name, we had the long form "limni" and the long form "pota", indicating that the last polyomino is attached to the middle one rather than the initial one. In general, each new polyomino is attached to the most recent one with a long form; this rule indicates the default parenthesization.
It is sometimes necessary to parenthesize explicitly, even with the above rule. For example, we cannot yet distinguish the names of ${}_4B_2 ( {}\mathop{+}_1 {}_5A\ ( {}\mathop{+}_3 {}_1A\ {}\mathop{+}_5 {}_1A\ ))$ and ${}_4B_2 ( {}\mathop{+}_1 {}_5A\ ( {}\mathop{+}_3 {}_1A\ ) {}\mathop{+}_5 {}_1A\ )$. The former is called tetralimnihensypentapotatrisypentasy, since by default the final block (the omitted "henpo" in "pentasyhenpo") is attached to the most recent long-form "pentapota". To override this default parenthesization, we can surround an inner expression with "ex" and "ter". So the latter polyomino, ${}_4B_2 ( {}\mathop{+}_1 {}_5A\ ( {}\mathop{+}_3 {}_1A\ ) {}\mathop{+}_5 {}_1A\ )$, is called tetralimnihensyexpentapotatrisyterpentasy, to indicate that the "pentapotatrisy" and the omitted "henpo" are being hensy-attached and pentasy-attached to the base "tetralimni".
For rings defined by the polyominos they surround, we can use the suffix "ni" (from "nisi", island). The polyomino below is called tripodidexni. If other polyominos are attached to an island one, the long form "nisi" is used in place of "ni".
Here are the names of all the pentominoes, listed by row in the order drawn below.
Other shortcuts could be proposed, such as contracting "ardex" to "ax" and "dexar" to "der". I think I'll stop here though.
Redelmeier's Algorithm is a traditional polyomino enumeration algorithm. It produces each polyomino once, and only once. Hence, it is suited to naming polyominoes. The following will give an injection from the set of polyominoes into the set of all finite sequences of positive integers.
Redelmeier's Algorithm: For first description, see Counting Polyominoes: Yet another attack by Hugh Redelmeier 1981. A description is also given here: https://www.csun.edu/~ctoth/Handbook/chap14.pdf.
This enumeration procedure arranges polyominoes in a tree. Each n-omino is a parent to finitely many (n+1)-ominoes, each child is reached by adding a specific allowable cell. Define the monomino to have name-sequence $\{0\}$, and say inductively that if $\{0, s_1, s_2, \cdots, s_n\}$ is the name-sequence for an n-omino, adding the lexicographically j-th allowable cell by Redelmeier's Algorithm yields the polyomino with name-sequence $\{0, s_1, s_2, \cdots, s_n, j\}$.
Notice this scheme will name fixed polyominoes, not free ones.
