Ellipse in polar coordinates

Question

I think Wikipedia's polar coordinate elliptical equation isn't correct. Here is my explanation: Imagine constants $a$ and $b$ in this format -

Where $2a$ is the total height of the ellipse and $2b$ being the total width. You can then find the radial length, $r$, at any angle $\theta$ to major axis as...

$$r(\theta) = \sqrt{(b \sin(\theta))^2 + (a \cos(\theta))^2}$$

...by just following the Pythagorean theorem. Yet Wikipedia's equation for the polar coordinate ellipse is as follows:

$$r(\theta) = \frac{ab}{\sqrt{(b \cos(\theta))^2 + (a \sin(\theta))^2}}$$

Here is the link to the Wikipedia page: Can someone explain this, please? Why divide by the hypotenuse? Why the $ab$? Thank you!

Answer 1

It's easiest to start with the equation for the ellipse in rectangular coordinates:

$$(x/a)^2 + (y/b)^2 = 1$$

Then substitute $x = r(\theta)\cos\theta$ and $y = r(\theta)\sin\theta$ and solve for $r(\theta)$.

That will give you the equation you found on Wikipedia.

Answer 2

Polar Equation from the Center of the Ellipse

The equation of an ellipse is $$ \left(\frac{x}{a}\right)^2+\left(\frac{y}{a\sqrt{1-e^2}}\right)^2=1\tag1 $$ Using $x=r\cos(\theta)$ and $y=r\sin(\theta)$ in $(1)$, we get $$ r^2\cos^2(\theta)+\frac{r^2\sin^2(\theta)}{1-e^2}=a^2\tag2 $$ and we can solve $(2)$ for $r^2$ to get the polar equation $$ r^2=\frac{\overbrace{a^2\!\left(1-e^2\right)}^{b^2}}{1-e^2\cos^2(\theta)}\tag3 $$

---

Polar Equation from a Focus of the Ellipse

Centered at the right focus $$ \left(\frac{x+ae}a\right)^2+\left(\frac{y}{a\sqrt{1-e^2}}\right)^2=1\tag4 $$ Using $x=r\cos(\theta)$ and $y=r\sin(\theta)$ in $(4)$, we get $$ r^2\cos^2(\theta)+2aer\cos(\theta)+a^2e^2+\frac{r^2\sin^2(\theta)}{1-e^2}=a^2\tag5 $$ which gives the quadratic equation in $r$: $$ \frac{r^2\left(1-e^2\cos^2(\theta)\right)}{1-e^2}+2aer\cos(\theta)-a^2\!\left(1-e^2\right)=0\tag6 $$ whose solution is $$ r=\frac{a\!\left(1-e^2\right)}{1+e\cos(\theta)}\tag7 $$

Answer 3

EDIT1:

What you at first proposed as ellipse looks like:

The Ellipse parametrization is done differently. To more clearly distinguish between them we should note there are two different $\theta$ s, viz $\theta_{deLaHire}$ and the standard polar coordinate $\theta_{polar}$ used for central conics, ellipse in this case. We are not referring to the Newton Ellipse as there is no query about it.

The first angle denotes by $ \theta_{deLaHire}$.

A radial line was constructed by deLaHire originally commences at a slightly bigger angle $\theta_{\text{deLaHire}};$ (red lines) each point $E$ on ellipse in first quadrant is reached by drawing vertical and horizontal lines from points of intersection of this polar/radial line with the two circles radii $(a,b)$ at $(P,Q)$, to meet at E as shown.

$$ x= a \cos\theta_{deLaHire}\; ; y=b \sin\theta_{deLaHire}\;;\tag1 $$

The second angle is used in polar coordinates in the standard ellipse and is measured from center of the circles. We call it $\theta_{polar}$ as usual. Green radial line.

For an ellipse axes $(a,b)$ along $(x,y)$ coordinate axes respectively centered at origin given Wiki expression is obtained in polar coordinates thus:

Plug in

$$ x=r_{polar}\cos \theta_{polar};\, y=r_{polar}\sin \theta_{polar} ; $$

casting the standard equation of an ellipse from Cartesian form:

$$ \left(\frac{x}{a}\right)^2+\left(\frac{y}{b}\right)^2 =1 $$

to get

$$ OE =r_{polar}= \frac{ab}{\sqrt{(b \cos \theta_{polar})^2 + (a \sin \theta_{polar})^2}} \tag 2 $$

In either case polar angles $\theta = 0$ and $\theta= \pi/2$ reach to the same points at the ends of major and minor axes respectively. The angle variations are plotted showing by comparison that starting deLaHire polar line is inclined more than (or equals to at extreme axes) the Central polar coordinate always. Can you figure out errors in the second and fourth quadrants?

Sketched Ellipse dimensions are $(a=5,b=3,e=0.8)$.

Answer 4

You're making the common mistake of using the polar coordinate instead of the eccentric anomaly which is the parameter in the ellipse coordinates.

Answer 5

To derive the polar coordinates of an ellipse, I believe it is simpler to start from a geometric perspective rather than an algebraic one. If you begin with the equation

$$ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $$

you will encounter a quadratic equation. While this approach will ultimately yield the correct result, it involves quite a bit of computation. A geometric approach, on the other hand, simplifies the process.

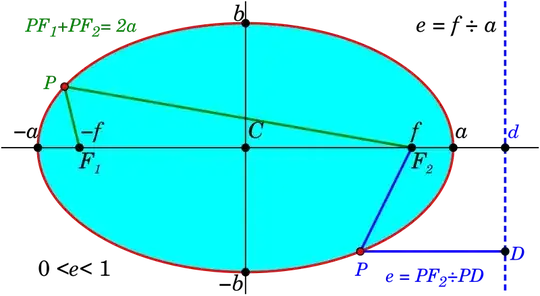
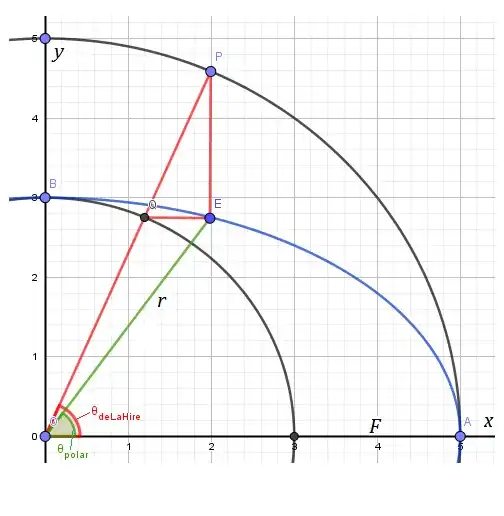
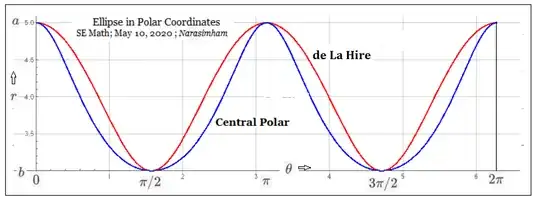
Let us consider the polar form centered at the left focus of a horizontal ellipse.

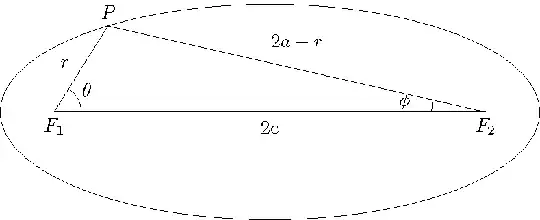
Define the major axis length of the ellipse as $2a$. Let $P$ be an arbitrary point on the ellipse, and let $F_1$ and $F_2$ be the foci. Denote $PF_1 = r$ and $PF_2 = 2a - r$. Define the angles $\angle PF_1F_2 = \theta$ and $\angle PF_2F_1 = \phi$.

By the Law of Sines, we have

$$ \frac{r}{\sin\phi}=\frac{2a-r}{\sin\theta} $$

Rearranging gives

$$ \sin\phi=\frac{r\sin\theta}{2a-r} $$

Using the identity $\cos^2\phi+\sin^2\phi=1$, we obtain

$$ \cos^2\phi+\frac{r^2\sin^2\theta}{(2a-r)^2}=1 $$

which simplifies to

$$ \cos\phi=\sqrt{1-\frac{r^2\sin^2\theta}{(2a-r)^2}} $$

Next, we use the equation

$$ r\cos\theta+(2a-r)\cos\phi=2c $$

Substituting $\cos\phi$ with $\sqrt{1-\frac{r^2\sin^2\theta}{(2a-r)^2}}$, we get

$$ r\cos\theta+(2a-r)(\sqrt{1-\frac{r^2\sin^2\theta}{(2a-r)^2}})=2c $$

Rearranging,

$$ 2c-r\cos\theta=(2a-r)(\sqrt{1-\frac{r^2\sin^2\theta}{(2a-r)^2}}) $$

Squaring both sides, we obtain

$$ (2c-r\cos\theta)^2=(2a-r)^2-r^2\sin^2\theta $$

$$ \implies r^2\cos^2\theta-4cr\cos\theta+4c^2=4a^2-4ar+r^2-r^2\sin^2\theta $$

$$ \implies r^2(\cos^2\theta+\sin^2\theta-1)+r(-4c\cos\theta+4a)=4a^2-4c^2 $$

It is satisfying to see that the term $\cos^2\theta+\sin^2\theta-1=0$, eliminating $r^2$. This simplifies to

$$ r(-4c\cos\theta+4a)=4a^2-4c^2 $$

$$ \implies r=\frac{4a^2-4c^2}{-4c\cos\theta+4a} =\frac{a^2-c^2}{a-c\cos\theta} $$

Using $c=a\epsilon$, we express this in terms of the eccentricity:

$$ r=\frac{a^2-c^2}{a-c\cos\theta}=\frac{a^2-a^2\epsilon^2}{a-a\epsilon\cos\theta}=\frac{a(1-\epsilon^2)}{1-\epsilon\cos\theta} $$

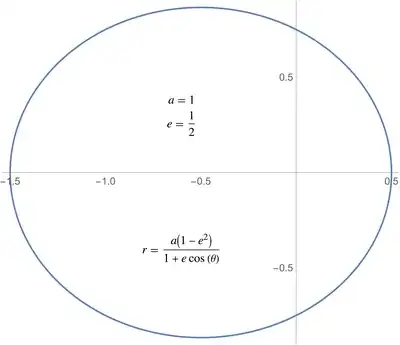
This is the form when centered at the left focus. If instead we center at the right focus and follow the same steps, we obtain

$$ r=\frac{a(1-\epsilon^2)}{1+\epsilon\cos\theta} $$

This geometric approach also extends naturally to hyperbolas and parabolas. Its main advantage is that it avoids solving a complicated quadratic equation. I hope this helps!