13

$\newcommand{\nest}{\operatorname{nest}}$Let's define a function $\nest(f, x, k)$, which takes a function $f$, an input $x$, and a non-negative integer $k$, and calls $f$ on $x$ repeatedly ($k$ times). For example, $$ \nest(f, x, 0) = x\\ \nest(f, x, 1)=f(x)\\ \nest(f, x, 2)=f(f(x))\\ \nest(f, x, 3)=f(f(f(x)))$$ Formally, this function can be written as $$ \nest(f, x, k)= \begin{cases} x & \text{if } k=0\\ \nest(f, f(x), k-1) & \text{otherwise} \end{cases}$$

For a given $k$ and a polynomial $p$, how can I find a function $f: \mathbb C \to \mathbb C$ such that $\nest(f, x, k)=p(x)$?

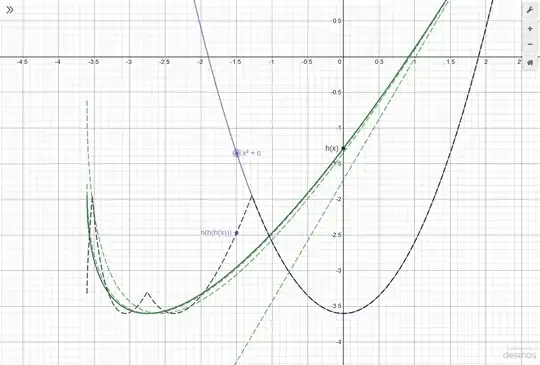
If it's not possible to do so in the general case, is it possible with $p(x)=c+x^2$?

Simply Beautiful Art
  • 76,603
Antonio Perez
  • 249
  • 1
  • 2
  • 2
    I don't know about $c+x^2$ but I found the function $f(x)=\sqrt{x^2+\frac{c}{k}}$ for $p(x)=\sqrt{c+x^2}$ – Shrey Joshi Jul 19 '18 at 20:11
  • 2
    It's not to hard to find a function $f$ of that sort. For $k = 2$, for example, start with two arbitrary numbers $a$ and $b$, and define $f$ to act according to the chain $a \mapsto b \mapsto a^2 +c \mapsto b^2 + c \mapsto (a^2 + c)^2 + c \mapsto \cdots$. Then take two other starting numbers that don't appear in that chain and repeat. (If separate chains eventually overlap, then join them into a tree structure.) Whether any function $f$ with a remotely interesting functional form exists, of course, is a different question. – Connor Harris Jul 19 '18 at 20:17
  • 2
    Doubt you can find one for $p(x)=c+x^2$. At least if you want $f$ to be holomorphic. Such functions fold the complex plane onto itself. Compositions will fold the plane a power of that original number. For example, if $f$ doesn't fold the plane, neither will any of its further nestings. If $f$ folds the complex plane with two layers, the 2nd nesting will fold the plane with four layers. $3$ layers will result in $9$ layers on the next nesting. $2$ is not a tenable power for foldings of a nesting. Probably can be made rigorous with the Argument principle. –  Jul 19 '18 at 20:29
  • I tried to find a series expansion for $f(x)$ with $k=2$ and $p(x)=1+x^2$ over $[0,1]$ using $11$ equally spaced points and minimizing the SSR. I get $f(x)\approx0.643+0.033x+0.940x^2-0.201x^3$. It fits so well that I'd assume $f(x)$ exists in this case. But whether it has a closed form or exists over all of $\mathbb{C}$ is another question. Regardless, you might be able to find approximations to your $f(x)$'s Graph: https://www.desmos.com/calculator/vf5fdpjbwi – Jam Jul 19 '18 at 20:41
  • There is no solution when $c=-2$ and $k=2$. – Arnaud Mortier Jul 19 '18 at 20:48
  • 3
    What you're looking for are called fractional iterates of the (polynomial) function; see e.g. this WIkipedia bit or this one or this previous math.se question – Steven Stadnicki Jul 19 '18 at 21:06

3 Answers3

4

You are really asking about functional iterates, normally denoted by $f^ n(x)\equiv \operatorname{nest}(f, x, n)$. I gather you are interested in problem solving methods over rigor.

They are normally obtained by functional iteration through Schröder's equation, but even your simple quadratic $p(x)=x^2+c$ does not have closed solutions, except, e.g., for $c=-2$, a "chaotic" logistic map , as you may see from the examples in the WP article linked above.

In that celebrated special case, a closed form (p302) was found by Ernst Schroeder himself (1870).

Namely, for
$$ p(x)= x^2-2, $$ it follows directly that for $$ y=\frac{x\pm \sqrt{x^2-4}}{2} $$ that is $$ x=y+y^{-1}, $$ one has $$ p(x)=y^2+y^{-2}\equiv p^1 (x). $$ Whence,
$$ p^n (x)= y^{2^n}+ y^{-2^n}. $$

More formally, in E.S.'s language of conjugacy, $$ \psi(p(x))=g(\psi(x)),\\ \psi(x)=\frac{x\pm \sqrt{x^2-4}}{2}\\ g(y)=y^2 \qquad \Longrightarrow \\ g^n(y)=y^{2^n};$$ so that $p(x)= \psi^{-1} \circ g \circ \psi (x)$, and $$p^n= \psi^{-1} \circ g^n \circ \psi ~.$$

I am restricting this to real variables and domains where the objects treated make sense. Your particular question $f^k (x)=x^2-2=p(x)$ then can produce $p^{1/k}(x)$ for suitable domains for you to explore. There are, of course, a plethora of solution-seeking texts on the subject, like C Efthimiou's Introduction to Functional Equations, AMS 2011, ISBN: 978-0-8218-5314-6 , online. A conjugacy iteration approximation method is available in our 2011 paper: Approximate solutions of Functional equations.

Simply Beautiful Art
  • 76,603
Cosmas Zachos
  • 6,223
  • 1
    Not sure that you present Schroeder's example at the end in an optimal way, anecdotally because you seem to use the notation $f$ for another object than the OP, and mainly because your function $\psi$ is not defined unambiguously. Remember that the OP asks for some function $f:\mathbb C\to\mathbb C$ such that $f(f(z))=p(z)$ for every $z$ in $\mathbb C$, where $p:\mathbb C\to\mathbb C$ denotes the polynomial $p(z)=z^2-2$. Schroeder's approach (and everybody's approach after him) starts with the remark that, for every $z\ne0$, $$p(z+z^{-1})=z^2+z^{-2}$$ Thus, if one can find some ... – Did Jul 25 '18 at 18:41
  • 1
    ... function $\psi:\mathbb C\to\mathbb C^*$ such that, for every $z$ in $\mathbb C$, $$z=\psi(z)+\psi(z)^{-1}\tag{1}$$ then the function $f$ defined formally by $$f(z)=\psi(z)^{\sqrt2}+\psi(z)^{-\sqrt2}$$ is a solution. Now, this approach obviously meets some serious problems that must be solved before one can consider that it addresses the question, such as the fact that, for every complex number $z$ not in the subset $[2,+\infty)$ of the real line, no solution $\psi(z)$ of the identity $(1)$ is real and nonnegative hence, one must explain how one should define $\psi(z)^\sqrt2$, ... – Did Jul 25 '18 at 18:41
  • ... since $\sqrt2$ is not an integer. These aspects of the problem surely can be straightened out, but such a work is not done in your answer. – Did Jul 25 '18 at 18:42
  • "I'm not sure what you are objecting to" ?? Did you read my comments? – Did Jul 25 '18 at 18:59
  • 1
    I mean, in routine physics applications, one restricts to real fields and avoids juicy definitional ambiguities of plain powers, the case for $\psi^{1/k}$... – Cosmas Zachos Jul 25 '18 at 19:00
  • That may be the case, but, first, "routine physics applications" are not all there is in this world and, second, the OP explicitely asked for solutions $f:\mathbb C\to\mathbb C$. – Did Jul 25 '18 at 19:02
  • Ah... I read the question much more broadly... He clearly does not know what one learns in basic practical overviews of functional iterations, probably in computer science, and how one restricts domains and ranges to get anything at all. My sense is that restricting the problem to something arbitrary right from the start will limit his options. People write books on functional iterates of quadratic maps, and expecting anything beyond anecdotal "success stories" might be over-reaching. – Cosmas Zachos Jul 25 '18 at 19:08
  • 1
    FYI, even restricting things to $\mathbb R$, there is actually no solution to the equation $f(f(x))=x^2-2$ for every $x$ in $\mathbb R$. See there for some explanations. – Did Jul 25 '18 at 19:24
  • And I see that you plagiarize your own answers... Not nice. – Did Jul 25 '18 at 19:26
  • My comments there did not indicate my appreciation of the domains? You expect me to steer him to Conway's solution? That is the point of "suitable domains". As for "self-plagiarism", well, this is a more apposite venue than that, and I am citing, chapter and verse, the real discoverer, E.S. (1870), unlike the other answers. I suspect the OP will learn something about Julia sets. – Cosmas Zachos Jul 25 '18 at 19:38
  • 1
    How are Julia sets related to the (in)existence of a functional square root of $x\mapsto x^2-2$? – Did Jul 25 '18 at 19:48
1

I will discuss quadratic $p(x)$, although the general method applies to $p(x)$ with an attractive fixed point. First consider $p(x)=x(a-x)$, with $|a|<1$, then there is an attractive fixed point at $0$. We look for a function $H(x)$ such that equation 1 is obeyed:

$H(p(x))=aH(x)$. ( 1)

We can then put Equation 2:

$p^n(x)=H^{-1} (a^nH(x))$. ( 2)

It is straightforward to expand $H(x)$ as a power series $H(x)= x+x^2/(a(a-1)+...$, but the higher order terms are relatively complex rational functions of a.

One can compute $H(x)$ by computing $y=p^n(x)$ with $n$ sufficiently large that the power series is accurate for $H(y)$ then put $H(x)=a^{-n}H(y)$.

I did numerical experiments for $a=1/2$, and the taylor series for $H(x)$ out to order 10. Equation 1 was obeyed to high accuracy, $H(x)$ appears smooth on its domain, which is the basin of the 0 attractor. $H(x)$ is singular on the boundary of its domain, the Julia set, and I don't think it can be continued beyond there.

$H(x)=0$ for all 0's of $p^n(x)=0$ and any integer $n$. It appears to be analytic on its domain. Equation 2 allows us to differentiate with respect to n and create a continuous flow map in the complex plane. I have not had time to study the inverse map. Clearly it must be multiple valued, but I believe it has regions where single valued definitions exist. In particular, for $p^n(x)=H^{-1} (a^nH(x))$ and $n$ small, we can use $x$ as the starting point of an iterative method to find $H^{-1} (a^nH(x))$.

The function $x^2+c$ has a quadratic fixed point at $\infty$. In this case we transform the mapping to $q(x)=x^2/(1+cx^2)$ and develop a power series about $0$. Because the fixed point is quadratic the functional equation is different. I have not studied this case much yet.

tippy2tina
  • 644
0

Similar to tippy2tina's answer, one can easily numerically generate such functions on $\mathbb R$ when they converge monotonically to a fixed-point if a fixed-point exists. Let $f^k(x)=\operatorname{nest}(f,x,k)$. In this case consider for $c\le-1/4$:

$$p(x)=x^2+c,\\q(x)=p^{-1}(x)=\sqrt{x-c}$$

where the inverse, $q$, has $q^n(x)\to\beta=\frac{1+\sqrt{1-4c}}2$ monotonically and

$$q'(\beta)=\frac1{2\beta}$$

describing its rate of convergence

$$q^{n+1}(x)-\beta\sim\frac{q^n(x)-\beta}{2\beta}$$

which implies we can have

$$q^{n+\alpha}(x)-\beta\sim\frac{q^n(x)-\beta}{(2\beta)^\alpha}$$

and thus we may define

$$q^\alpha(x)=\lim_{n\to\infty}p^n\left(\beta+\frac{q^n(x)-\beta}{(2\beta)^\alpha}\right)$$

In your case, you desire to find

$$p^{1/k}(x)=q^{-1/k}(x)=\lim_{n\to\infty}p^n\left(\beta+\frac{q^n(x)-\beta}{(2\beta)^{-1/k}}\right)$$

which will converge to a real solution over $[a,\infty)$ for some $a\le0$. Note that $p$ has two inverses, so only a part of the solution is accounted for, while the other part cannot be real due to issues described in the linked posts.

Graphically for solving in the case of $c=-3.6$ and $k=3:$

enter image description here

Simply Beautiful Art
  • 76,603