During my recent work I encountered a weird type of differential equation containing scalar factors. In order to understand them better I thought it would make sense to look at a simpler example like:
$$ \dot x(t) = x(2t)$$
How does one solve this equation? Does it even have a solution? It seems kinda related to Functional Differential Equations which I am not familiar with.
Disclaimer: It is not a complete answer, but the development of an idea. I encourage anyone who wants to edit and complement this answer. Furthermore, I have no experience with functional differential equations.
Supposing that our solution is an analytical function of $t$, we write it as a power series $$ x(t) = \sum_{n=0}^\infty a_n t^n. $$ Substituting it in the equation, we get $$ \sum_{n=1}^\infty n a_n t^{n-1} = \sum_{n=0}^\infty a_n 2^n t^n, $$ then, changing the index, $$ \sum_{n=0}^\infty (n+1) a_{n+1} t^{n} = \sum_{n=0}^\infty a_n 2^n t^n, $$ which lead us to the following recurrence relation: $$ a_{n+1} = \frac{2^n}{n+1} a_n. $$
As pointed by Alex R. and by martin cohen, there is no analytical solution to the equation other than the trivial, (as suggested by Hans Engler).
Following the suggestion by Ivan Neretin, I used the idea from this answer to a similar question: Solving functional differential equation $f'(x)=2f(2x)-f(x)$
I will solve the more generic equation $\dot{x} = x(at)$. As pointed by Hyperplane, I will use the following series: $$ x = \sum_{n=-\infty}^\infty c_n \exp (-a^n t). $$ Therefore, $$ \dot{x} = -\sum_{n=-\infty}^\infty c_n a^n \exp (-a^n t), $$ $$ x(at) = \sum_{n=-\infty}^\infty c_n \exp (-a^{n+1} t) = \sum_{n=-\infty}^\infty c_{n-1} \exp (-a^n t). $$ Then, plugging in the equation, we get $$ -\sum_{n=-\infty}^\infty c_n a^n \exp (-a^n t) = \sum_{n=-\infty}^\infty c_{n-1} \exp (-a^n t), $$ which requires $$ \frac{c_n}{c_{n-1}} = -\frac{1}{a^n}. $$ Solving this recurrence relation with an "initial condition" $c_0 = A$, we get $$ c_m = A \prod_{n=0}^m \frac{c_n}{c_{n-1}} = A \prod_{n=0}^m -\frac{1}{a^n} = \frac{(-1)^m}{a^{m(m+1)/2}} A. $$ (See that $m(m+1)/2$ is the m-th triangular number). Therefore, our solution is $$ x = A \sum_{n=-\infty}^\infty \frac{(-1)^n}{a^{n(n+1)/2}} \exp (-a^n t), $$ which one can easily check to satisfy the equation. Since it is an alternating series, we can apply the Leibiniz criterion. The ratio between two consecutive terms is $a^{n+1} \exp(a^n(a-1)t)>1 \ \forall a>1$. Therefore, the series converges for $a>1$.
To obtain the value of $x(0)$ one must split the series: $$ x(0) = A \sum_{n=0}^\infty \frac{(-1)^n}{a^{n(n+1)/2}} + A \sum_{n=-1}^{-\infty} \frac{(-1)^n}{a^{n(n+1)/2}} = A \sum_{n=0}^\infty \frac{(-1)^n}{a^{n(n+1)/2}} + A \sum_{n=0}^{-\infty} \frac{(-1)^{n-1}}{a^{(n-1)n/2}} = $$ $$ A \sum_{n=0}^\infty \frac{(-1)^n}{a^{n(n+1)/2}} + A \sum_{n=0}^{\infty} \frac{(-1)^{-n-1}}{a^{-n(-n-1)/2}} = A \sum_{n=0}^\infty \frac{(-1)^n}{a^{n(n+1)/2}} - A \sum_{n=0}^{\infty} \frac{(-1)^{n}}{a^{n(n+1)/2}} = 0. $$
It is interesting to see the behavior of the derivatives of this function. We know that $\dot{x} = x(at)$. Differentiating it, we have
$$
\ddot{x} = \frac{d}{dt} x(at) = \frac{d(at)}{dt} \frac{d}{d(at)} x(at) = a \dot{x}(at) = a x(a^2 t),
$$
$$
\dddot{x} = \frac{d}{dt} a x(a^2 t) = a \frac{d(a^2t)}{dt} \frac{d}{d(a^2t)} x(a^2t) = a^3 \dot{x}(a^2t) = a^3 x(a^3 t),
$$
or, in general,
$$
x^{(n)} = a^{n(n-1)/2} x(a^n t),
$$
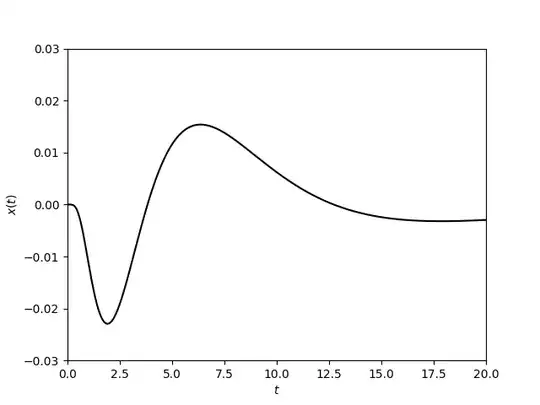
which can be readly proved by induction. Therefore, it is easy to see that $x^{(n)}(0) = 0$ for all $n$, i.e., showing that the solution is non-analytical at $t=0$. Here is the graph of the solution for $a=2$ and $A=1$.
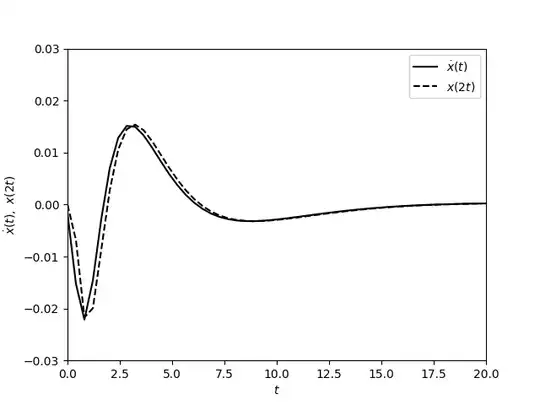
And here is a graph comparing $\dot{x}(t)$ to $x(2t)$. This graph is rougher on purpose to allow an easy distinction between both curves. For a thinner resolution, the matching is perfect.
I also tried to solve the equation numerically using a simple finite differences scheme. Defining the domain as $t \in (0,T)$ and discretizing it in $N$ equally spaced points, the equation for the point $i$ is $$ x_{i+1} - x_i - hx_{[ai]} = 0, $$ in which $h$ is the step size, and $[ai]$ indicates that the result of $a\cdot i$ must be rounded to the closer integer. This method has a serious deficiency because the solution only will have mathematical meaning in the interval $t\in (0,T/a^2)$. That's because the finite differences equation can be applied only in the interval $t\in (0,T/a)$, as $x_{[ai]}$ would be undefined for $t>T/a$. Therefore, the equation for $t>T/a$ will not represent the original equation and will be only a "placeholder". However, the spurious solution in the region $T/a<t<T$ will cause an effect in the remaining part of the domain, specifically in the region $T/a^2<t<T/a$. Therefore, the solution only holds for $0<t<T/a^2$ and is spurious for $T/a^2<t<T$.
For numerical purposes, the matrix $A_{ij}$ is defined as $A_{ij} = A^1_{ij} + A^2_{ij}$, being $$ A^1_{ij} = \begin{cases} 1, & i+1=j \\ -1, & i=j \\ \end{cases}, \ \ \ A^2_{ij}=\begin{cases} -h, & [ai]=j \\ 0, & \mathrm{otherwise} \\ \end{cases}. $$
As the last line of $A^1_{ij}$ is undefined, it can be used to providing the "boundary" condition. It is important to notice that all solutions are equal up to a multiplicative constant. Therefore, the solution can be obtained by
$$
x_i = (A_{ij})^{-1} B_j,
$$
in which $B_j = 0$ for all $j$, except for the position in which the condition was imposed. Here is a numerical solution obtained for $a=2$, $h = 4\times 10^{-2}$ and $T=160$:
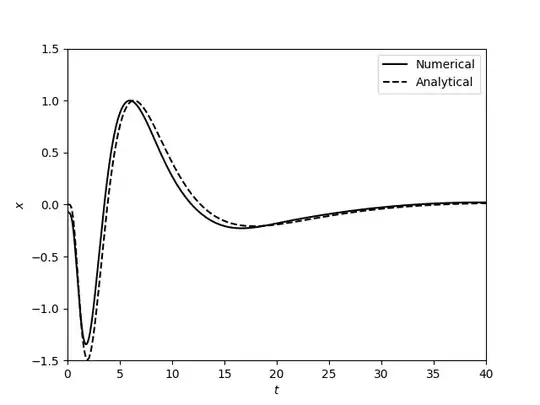
Both solutions were 'normalized' to allow a better comparison. There is a good agreement among the solutions. It is interesting to see that the numerical solution does not satisfy $x(0) = 0$, only approximately. It is also important that the domain be sufficiently large in order that the most relevant oscillations are contained in the region $0<t<T/a^2$. The size of the domain is more important to the accuracy of the solution than the step size.
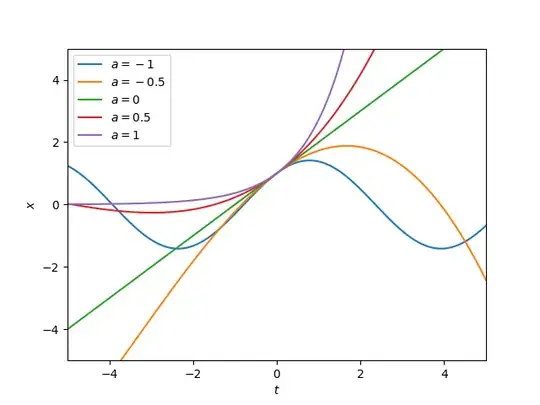
For $1\leq a\leq 1$ the power series solution,
$$
x = A\sum_{n=0}^\infty \frac{a^{n(n-1)/2}}{n!} t^n,
$$
converges. For $a=0$ the solution degenerates to $x=kt$, for $a=1$, to $x = k \exp t$ and for $a=-1$ to $x=k\sin (t+\pi/4)$ (I found this one quite surprising!). Solutions for intermediates values of $a$ are shown in the graph:
Secondly, this idea only supplies a non-trivial solution for $x(0)=0$, so the question about the case $x(0)=1$ remains open.
Anyway it seems like you had quite your fun with the problem :)
– Hyperplane Jun 06 '18 at 08:03Continuing rafa11111's answer, if $a_{n+1} = \frac{2^n}{n+1} a_n$ then $\dfrac{a_{n+1}}{a_n} = \dfrac{2^n}{n+1} $ so
$\begin{array}{} a_m &=& \Big(\prod\limits_{n=0}^{m-1} \dfrac{a_{n+1}}{a_n}\Big)\,a_0 &=& \Big(\prod\limits_{n=0}^{m-1} \dfrac{2^n}{n+1}\Big)\,a_0 &=& \dfrac{2^{m(m-1)/2}}{m!}\,a_0 &=& \dfrac{2^{T_{m-1}}}{m!}\,a_0 \end{array} $
Where $T_m$ is the $m$-th triangle number. This, as well as the obvious use of the ratio test, shows that the power series does not converge for any $x \ne 0$.
