6

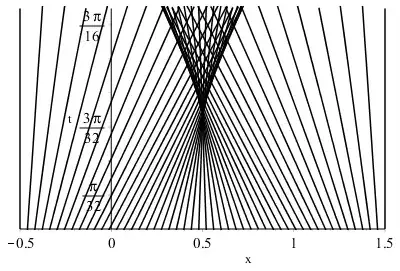
I have shown that a smooth solution of the problem $u_t+uu_x=0$ with $u(x,0)=\cos{(\pi x)}$ must satisfy the equation $u=\cos{[\pi (x-ut)]}$. Now I want to show that $u$ ceases to exist (as a single-valued continuous function) when $t=\frac{1}{\pi}$.

When $t=\frac{1}{\pi}$, then we get that $u=\cos{(\pi x-u)}$.

With single-valued function is it meant that the function is 1-1 ?

If so, then we have that $\cos{(2 \pi-u)}=\cos{(4 \pi -u)}$, i.e. for two different values of $x$, we get the same $u$, and so for $t=\frac{1}{\pi}$, $u$ is not 1-1.

But if this is meant, how are we sure that for $t \neq \frac{1}{\pi}$ the function is single-valued?

EditPiAf
  • 21,328
Evinda
  • 1,480

2 Answers2

8

The solution $u(x,t)$ is implicitly defined by the equation $F(x,t,u) = u - \cos\Big(\pi(x - ut)\Big) = 0$. The Implicit Function Theorem asserts that $F(x,t,u) = 0$ defines $u$ as a function of $x,t$ if $\dfrac{\partial F}{\partial u}\neq 0$, otherwise we expect characteristics to intersect (well, along a shock curve), i.e. $u(x,t)$ becomes multi-valued.

The partial derivative of $F$ with respect to $u$ is $$ \frac{\partial F}{\partial u}\colon = \partial_u F = 1 - \pi t\sin\Big(\pi(x-ut)\Big) $$ and along the characteristic $x = \cos(\pi x_0)t + x_0 = u(x_0,0)t + x_0$ for an arbitrary but fixed $x_0\in\mathbb{R}$ we have that $$ \partial_u F = 1 - \pi t\sin(\pi x_0). $$ It follows that $\partial_u F = 0$ whenever $$ t = \frac{1}{\pi\sin(\pi x_0)}. \tag{1}$$

Denote by $t^*$ the shortest time where $\partial_u F = 0$. Clearly, $\partial_u F\neq 0$ for all $t\ge 0$ if $$ \pi x_0\in [n\pi, (n+1)\pi], n=\pm 1,\pm 3, \pm 5, \dots, $$ so suppose not. It follows from $(1)$ that $$ t^* = \min_{x_0\in\mathbb{R}}\frac{1}{\pi\sin(\pi x_0)} = \frac{1}{\pi}. $$

Chee Han
  • 4,745
  • First of all, why do we consider $\frac{\partial{F}}{\partial{u}}$ along the characteristic line? Secondly, how do we deduce that $\frac{\partial{F}}{\partial{u}} \neq 0$ for all $t \geq 0$ if $\pi x_0 \in [n \pi, (n+1) \pi], n =\pm 1, \pm 3, \pm 5, \dots$ ? And also, how do we use this fact in order to find the shortest time? – Evinda May 28 '18 at 23:44
  • We exploit the fact that the solution is constant along the characteristics and so we may rewrite $x-ut$ as $x_0$ where $x_0$ is some initial point at $t=0$. 2) $\partial_u F\neq 0$ (actually, $\ge 1$) if the term $-\pi t\sin(\pi x_0)\ge 0$; since $t\ge 0$, it is enough to requiring $\sin(\pi x_0)\le 0$ which gives the desired ranges for $\pi x_0$.
    • – Chee Han May 29 '18 at 05:00
  • We look for shortest time because we are considering the worst case scenario, that is, when is the solution starting to become multi-valued? This follows from implicit function theorem, because it says that provided $\partial_u F\neq 0$, then locally we can write $u$ as a function of $x,t$. In particular, for each fixed time $T>0$, $u$ is a function of $x$. Of course, this will fail for $t\ge t^$ for some critical time $t^$.
    • – Chee Han May 29 '18 at 05:13
  • I have understood now how we get the ranges for $\pi x_0$, but I haven't understood how we get the shortest time when the solution is starting to become multi-valued. How do we use the implicit function theorem to deduce that the shortest time is $\frac{1}{\pi}$? Could you explain it further to me? @CheeHan – Evinda May 29 '18 at 07:15
  • For a fixed time $T>0$, the solution $u(x,T)$ fails to be single-valued when $u(x,T) = u(x)$ is not a function of $x$. But we do not have an explicit expression for the solution $u$ since it is defined implicitly by the equation $F(x,t,u) = 0$. Implicit function theorem says that $u$ is multi-valued if $\partial_u F = 0$, which is the case when $t = \frac{1}{\pi\sin(\pi x_0)}$ for some initial point $x_0$ and clearly the time depends on $x_0$, i.e. for each initial point $x_0$ there is a corresponding critical time, say $t_c$. – Chee Han May 29 '18 at 07:27
  • For instance, for $x_0 = 1/6$ we have $t_c = \frac{2}{\pi}$; for $x_0 = 1/4$ we have $t_c = \frac{\sqrt{2}}{\pi}$; for $x_0 = 1/3$ we have $t_c = \frac{2}{\sqrt{3}\pi}$. But we need to consider all characteristics, i.e. all possible initial points $x_0\in\mathbb{R}$. Since $t_c$ is inversely proportional to $\sin(\pi x_0)$, we want $x_0$ such that $\sin(\pi x_0)$ is the largest, i.e. when $x_0 = 1/2$ for example. This then gives the desired $t = \frac{1}{\pi}$. – Chee Han May 29 '18 at 07:35
  • Ok, I see... So we don't use somewhere the fact that $\partial_u{F} \neq 0$ for all $t \geq 0$ if $\pi x_0 \in [n \pi, (n+1) \pi], n=\pm 1, \pm 3, \pm 5, \dots$, do we? – Evinda May 29 '18 at 07:48
  • @Evinda Not really, that is just the special case that I pointed out. Sometimes we don't really consider all initial points $x_0\in\mathbb{R}$, but only on a certain interval, say $[a,b]$. If $[a,b]$ is one of these special intervals, then the solution is always single-valued; otherwise you can always find a critical threshold $t_c$ such that for all $t\ge t_c$, the solution becomes multi-valued. – Chee Han May 29 '18 at 08:30
  • So we see that for $t=\frac{1}{\pi}$ the solution is multi-valued iff $x_0$ is of the form $2n+\frac{1}{2}$ , right? – Evinda May 29 '18 at 09:34
  • @Evinda Yessss! – Chee Han May 29 '18 at 15:39