Doubling the cube with unit sticks

Question

In the January 2000 issue of Erich Friedman's Problem of the Month, the problem of bracing distances – building a rigid unit-distance graph where two vertices are the required distance apart – was considered. The first question there dealt with bracing polygons; it was pointed out that Maehara had proved in 1991 the equivalence of "braceable distances" with algebraic numbers. The easier second question dealt with bracing the square roots of integers using as few edges as possible.

One of Maehara's gadgets, the fan, allows dividing arbitrary angles into any number of equal parts; this also implies that all regular polygons can be braced. Since $\pi$ is transcendental, squaring the circle is obviously out of the question. Of the three main geometric problems of antiquity, doubling the cube remains; this is the focus of my question here.

What is the minimum number of unit edges required to brace $\sqrt[3]2$?

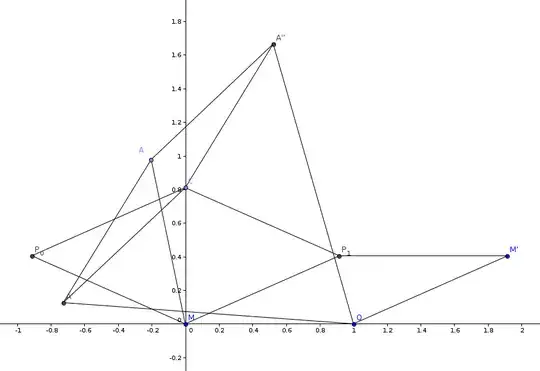
I had this neusis construction for the constant in the back of my head for a long while:

After some experimentation I obtained this variant suitable for implementation in the framework of bracing distances:

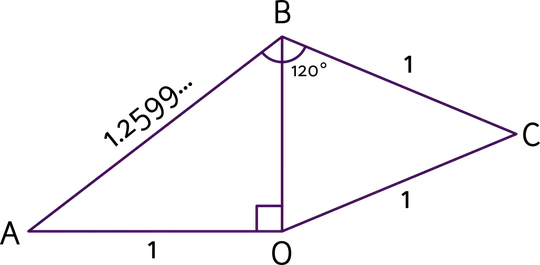
$\triangle AOB$ has $\angle AOB$ right and $AO=1$. $C$ lies on the other side of $OB$ from $A$ with $CB=CO=1$. If $\angle ABC=120^\circ$, $AB=\sqrt[3]2$. (This can be easily verified by erecting an equilateral triangle on $BC$, producing a new point $D$, then noting that $A,B,D$ are collinear and that $A,O,B,D$ in my diagram correspond to $A,C,G,H$ in the original. The latter's correctness has been verified here.)

I need to implement two constraints: $\angle AOB$ being right and $\angle ABC=120^\circ$. To do so, I turn to one of Maehara's gadgets, the jack:

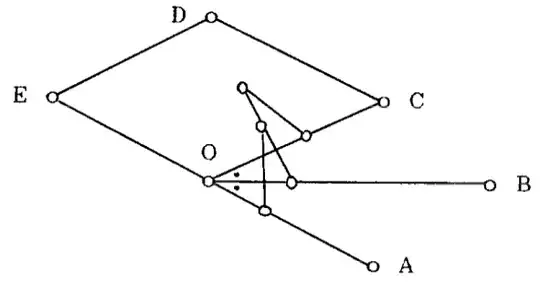
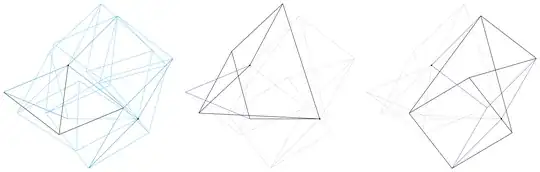
The part of this gadget between $O,A,B,C$ is what he calls the reverser, which forces $\angle COB=\angle BOA$. $AO$ is extended to $E$ and $OCDE$ is a rhombus; this forces $\angle BOD$ to be right while letting $OD$ vary. By a small modification to this gadget – defining $F$ on $OA$ and $G$ on $OC$ with $OF=OG$ and then erecting a rhombus $OFHG$ – I can also implement collinearity: $H$ must lie on the line defined by $OB$. Here are the standard and collinear jacks in my bracing of $\sqrt[3]2$, labelled with the corresponding points in my construction:

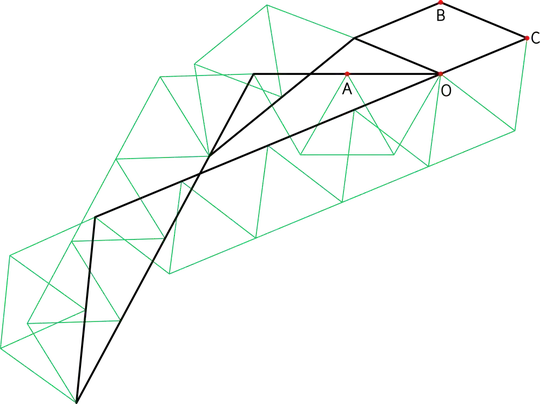
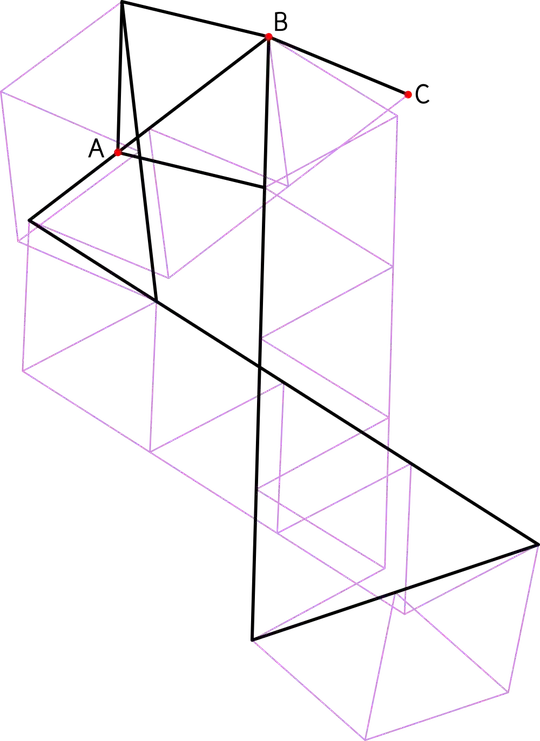
Note how $\angle ABC=120^\circ$ is enforced by a simple extension of the trusses keeping the jack's bars straight. This reuse of the intermediate points created when realising the gadgets is crucial to minimising the edge count.

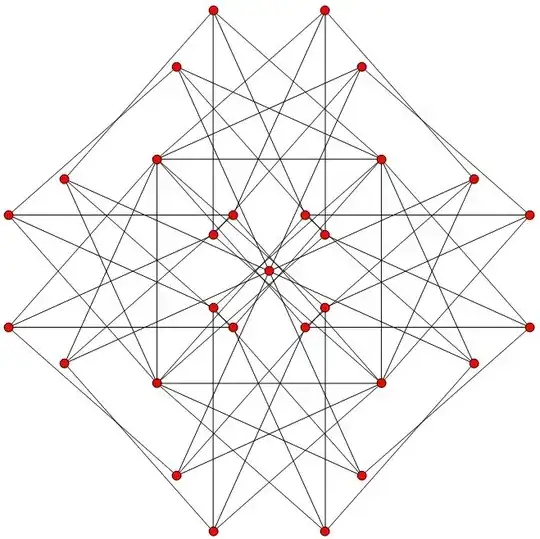
The whole framework uses 113 edges to brace $\sqrt[3]2$, highlighted below (SVG file here):

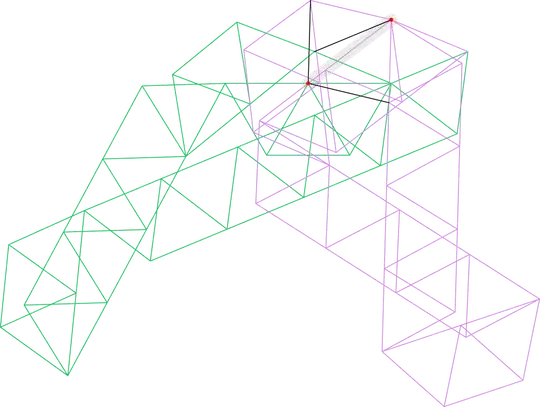
Is this optimal or can it be done better? Can fewer than 113 unit edges be linked into a rigid graph where two points are $\sqrt[3]2$ apart? Ed Pegg, this is your challenge.

Answer 1

Who, me? You think I can beat your nice construction within a matter of minutes? Okay, one $2^{1/3}$ polynomial we can look at is $1 - 3 x + 3 x^2 + x^3$, which has algebraic discriminant -108. If we can find braceable points that work nicely with that space, then getting back to $2^{1/3}$ should be easy. Here's some polynomials to extract complex roots from.

$$(x, 1 - 2 x + 2 x^2, 1 + 2 x + 2 x^2, 2 - 2 x + x^2 - 2 x^3 + 2 x^4, 2 + 2 x + x^2 + 2 x^3 + 2 x^4, 1 + 2 x + 6 x^2 - 16 x^3 + 8 x^4, 1 - 6 x + 14 x^2 - 8 x^3 + 8 x^4, 1 + 6 x + 14 x^2 + 8 x^3 + 8 x^4, 1 - 2 x + 6 x^2 + 16 x^3 + 8 x^4)$$

Find the points with unit distances and clean up, and you're left with the following unit-distance graph:

Is that rigid, or does it need more work? What is the chromatic number? Is it easy to get back to $2^{1/3}$? I don't know. But it's a nice graph within the correct algebraic space. See if it helps.

Answer 2

Khodulyov's bracings of regular polygons use a "folded" and very economical Peaucellier–Lipkin linkage that replicates the jack's functionality and then some. In the diagram below the long edges are of length $\sqrt3$ (five sticks in the actual realisation) and not only is $\angle P_0MO=\angle MOM'$ – $C$ is constrained to be on the perpendicular to $MO$ through $M$ and $P_0$ is constrained to be collinear with $P_1M$.

Combined with the question's strategy this gives a $43$-edge bracing of $\sqrt[3]2$ (the $\sqrt3$ diamonds in the second and third images below have been replaced with single edges for clarity):