Given $r > 0$, the solid:
$$
\Omega := \left\{(x,\,y,\,z) \in \mathbb{R}^3 : x^2 + y^2 \le r^2, \, x^2 + z^2 \le r^2\right\}
$$
is the intersection between two circular cylinders of radius $r$ and with perpendicular axes:
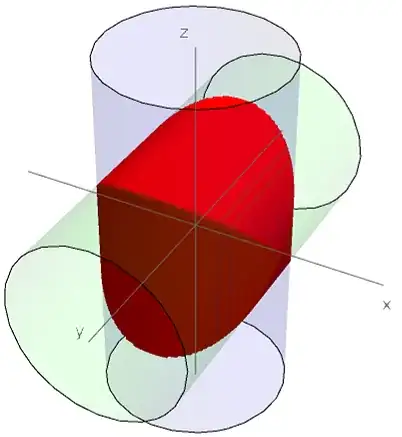
In particular, noting the three symmetries enjoyed by solid $\Omega$:
$$
(x,\,y,\,z) = \mathcal{S}(-x,\,y,\,z)\,,
\quad \quad
(x,\,y,\,z) = \mathcal{S}(x,\,-y,\,z)\,,
\quad \quad
(x,\,y,\,z) = \mathcal{S}(x,\,y,\,-z)
$$
the measure of this solid is equal to:
$$
||\Omega|| := \iiint\limits_{\Omega} 1\,\text{d}x\,\text{d}y\,\text{d}z
= 2^3\iiint\limits_{\Omega^*} 1\,\text{d}x\,\text{d}y\,\text{d}z
$$
where:
$$
\Omega^* := \left\{(x,\,y,\,z) \in \mathbb{R}^3 : x^2 + y^2 \le r^2, \, x^2 + z^2 \le r^2, \, x \ge 0, \, y \ge 0, \, z \ge 0\right\}.
$$
This done, through a coordinate transformation of the type:
$$
\small
(x,\,y,\,z) = (u\,r\,\cos v,\,u\,r\,\sin v,\,w)
\quad \text{with} \;
(u,\,v,\,w) \in \left[0,\,1\right] \times \left[0,\,\frac{\pi}{2}\right] \times \left[0,\,r\sqrt{1 - u^2\cos^2 v}\right]
$$
we have:
$$
||\Omega|| = 8\int_0^{\frac{\pi}{2}}\,\text{d}v \int_0^1 r^2\,u\,\text{d}u \int_0^{r\sqrt{1-u^2\cos^2 v}} \text{d}w = \frac{16}{3}\,r^3\,.
$$
As for the boundary of solid $\Omega$, we have:
$$
\partial\Omega := \Sigma_1 \cup \Sigma_2
$$
where:
$$
\begin{aligned}
& \Sigma_1 := \left\{(x,\,y,\,z) \in \mathbb{R}^3 : x^2 + y^2 = r^2, \, x^2 + z^2 \le r^2\right\}; \\
\\
& \Sigma_2 := \left\{(x,\,y,\,z) \in \mathbb{R}^3 : x^2 + z^2 = r^2, \, x^2 + y^2 \le r^2\right\}; \\
\end{aligned}
$$
which for the above symmetries implies:
$$
||\partial\Omega|| := \iint\limits_{\partial\Omega} 1\,\text{d}\Omega = 2\iint\limits_{\partial\Sigma_1} 1\,\text{d}\Sigma = 2 \cdot 2^3 \iint\limits_{\partial\Sigma_1^*} 1\,\text{d}\Sigma
$$
where:
$$
\Sigma_1^* := \left\{(x,\,y,\,z) \in \mathbb{R}^3 : x^2 + y^2 = r^2, \, x^2 + z^2 \le r^2, \, x \ge 0, \, y \ge 0, \, z \ge 0\right\}.
$$
This done, through a coordinate transformation of the type:
$$
(x,\,y,\,z) = (r\,\cos v,\,r\,\sin v,\,u)
\quad \text{with} \;
(u,\,v) \in \left[0,\,r\,\sin v\right] \times \left[0,\,\frac{\pi}{2}\right]
$$
we have:
$$
||\partial\Omega|| = 16 \int_0^{\frac{\pi}{2}} \text{d}v \int_0^{r\sin v} r\,\text{d}u = 16\,r^2\,.
$$
All this verifies what has been reported about the Steinmetz solid, as noted in the comments.
