6

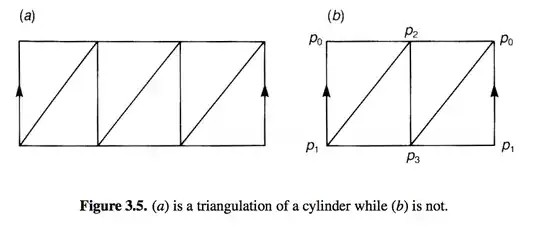
enter image description here

enter image description here

This is an example of triangulation of simplex from the book by M. Nakahara. This example is of an unoriented simplex. It says that $\langle p_0\rangle\cup\langle p_2\rangle$ is not a simplex, why not, they both are points and points are valid simplex. I am assuming that points taken together do not constitute a simplex.

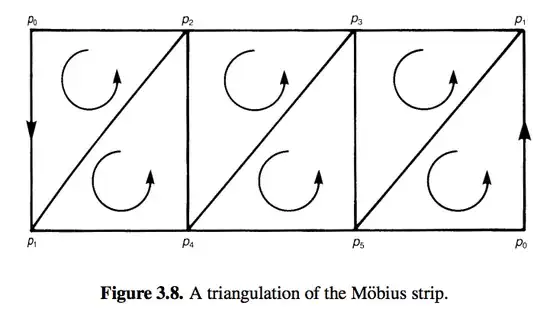
To further argue, following is a triangulation of Mobius strip. enter image description here

$(p_0p_1p_2) \bigcap (p_1p_4p_2)=p_1\cup p_2\cup(p_1p_2)$

Here also I am getting two points ($0$-simplex) in union form but it is valid, but in the first diagram it is invalid, why? The only way I can understand it as $p_1\cup p_2\cup(p_1p_2)=(p_1p_2)$ - can we do things like this. Because if this is so, we are "unionizing" simplexes of different dimensions and putting it as a single simplex. Is it even valid?

What am I getting wrong here? Your support is greatly appreciated.

Ivan
  • 508
user3001408
  • 857
  • In the second case the intersection of the two $2$-simplices is $(p_1,p_2)$, which is a $1$-simplex. – s.harp Nov 20 '17 at 13:03
  • 1
    In $(b)$ shouldn't the intersection of the two simplices $\sigma_2$ and $\sigma_{2'}$ be $(p_0,p_2)$? – SHASHANK PATHAK Sep 08 '20 at 07:11
  • @SHASHANKPATHAK did you figure out why the intersection is not $(p_0,p_2)$? – Ivan Oct 26 '22 at 15:09
  • @Ivan if you imagine joining the identified sides to form the actual cylinder, then we have the 1-simplex $(p_0, p_2)$ corresponding to half of the "upper" boundary circle of the cylinder, and the 1-simplex $(p_2, p_0)$ corresponding to the other half of the "upper" boundary circle. The intersection of the two 2-simplices is just two vertices, rather than $(p_0, p_2)$, because $(p_0, p_2)$ and $(p_2, p_0)$ are different 1-simplices. Hopefully this helps! – isaacholt100 Feb 06 '24 at 11:42

1 Answers1

4

For this ($K$) to be a triangulation note that

If $\sigma$ and $\sigma'$ are two simplexes of $K$, the intersection $\sigma \cap \sigma'$ is either empty or a common face of $\sigma$ and $\sigma'$, that is, if $\sigma,\sigma'\in K$ then either $\sigma\cap\sigma' = \emptyset$ or $\sigma\cap\sigma' \leq \sigma$ and $\sigma\cap\sigma' \leq \sigma'$

In this example $\sigma\cap\sigma = \langle p_0\rangle \cup \langle p_2\rangle$. You are right in the sense that both $\langle p_0\rangle$ and $\langle p_2\rangle$ are simplexes on their own. But $\langle p_0\rangle \cup \langle p_2\rangle$ is not a face of neither $\langle p_0p_1p_2\rangle$ or $\langle p_2p_3p_0\rangle$

caverac
  • 19,783
  • Could you explain why the intersection is $\langle p_0\rangle \cup \langle p_2\rangle $ instead of $\langle p_0,p_2\rangle$? – Ivan Oct 26 '22 at 15:11
  • @Ivan This is 2 years late, so I'm not sure to what extent it would be beneficial to you specifically but there are no 1-simplexes in common between $p_0 p_1 p_2$ and $p_2 p_3 p_0$. All that is in common between them is just the vertices $p_0$ and $p_2$ (the union of which is not a simplex). In the other example, you had an entire 1 simplex in common. – weirdmath Aug 22 '24 at 19:01