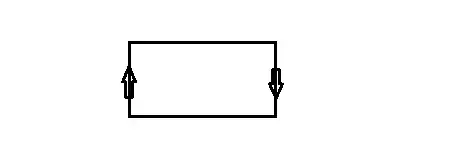
Let $W=[0,1]\times[0,1]$, where $(0,y)\sim(1,1-y)$ for all $0\leq y\leq 1$. Calculate the homology groups of $W$
I am a little confused with this exercise, I do not know how many vertices there are, nor 1-simplices, nor 2-simplices, could someone tell me this and the orientations? I think with this I could calculate the homology groups. Thank you very much