0

Definition 3.2. The $r$-chain group $C_{r}(K)$ of a simplicial complex $K$ is a free Abelian group generated by the oriented $r$-simplexes of $K$. If $r>\operatorname{dim} K, C_{r}(K)$ is defined to be 0 . An element of $C_{r}(K)$ is called an $r$-chain.

Let there be $I_{r} $ r-simplexes in $K$. We denote each of them by $\sigma_{r, i}(1 \leq i \leq$ $\left.I_{r}\right)$. Then $c \in C_{r}(K)$ is expressed as $$ c=\sum_{i=1}^{I_{r}} c_{i} \sigma_{r, i} \quad c_{i} \in \mathbb{Z} . $$

Page-102, Geometry, Topology and Physics, Second Edition

I don't understand this sum is we are taking. I understand that $\sigma$ is a r-simplex, but what's the idea behind multiplying a bunch of permutations by coefficient and adding them up..? How do I think of this and why is it important?

Clemens Bartholdy
  • 14,222
  • 2
    $\sigma$ is not a permutation -- it's an $r$-simplex. So we're looking at sums of simplices. Why this is an interesting thing to do depends on exactly what you're studying, but one reason is that they're the things we can integrate $r$-forms over. – Chris Grossack Jul 21 '22 at 02:11
  • Hmm I'll ahve to check my book again. – Clemens Bartholdy Jul 21 '22 at 02:14
  • 1
    Do you know what the "free abelian group generated by a set of objects" is? As a test, what is the free abelian group generated by ${mouse, banana, ear}$? – JonathanZ Jul 21 '22 at 02:27
  • I actually skipped over that section but I see now, it is actually the free abelian group generated by r- simplices. For your example x mouse + y banana + z ear (?) – Clemens Bartholdy Jul 21 '22 at 02:32
  • I am study about homology group – Clemens Bartholdy Jul 21 '22 at 02:33
  • 2
    Yep, that's right. At this point of the construction we're not using anything special about the simplices, and they might as well be a banana or an ear. When you want to define the boundary operator their simplishisness (simplicity?) will be used. – JonathanZ Jul 21 '22 at 02:36
  • Pretty profound point actually @JonathanZsupportsMonicaC – Clemens Bartholdy Jul 21 '22 at 22:29
  • Well, I though it was worth making. :-) – JonathanZ Jul 21 '22 at 23:16

1 Answers1

1

The operative term here is "free Abelian group". It basically encodes the idea of "multiplying a bunch of things by coefficients and adding them up". To echo @HallaSurvivor in the comments, the reason you might want this will depend on the specific application.

In the simplicial case, the interpretation is actually relatively intuitive. Let's take this example from a few sections later in Nakahara.

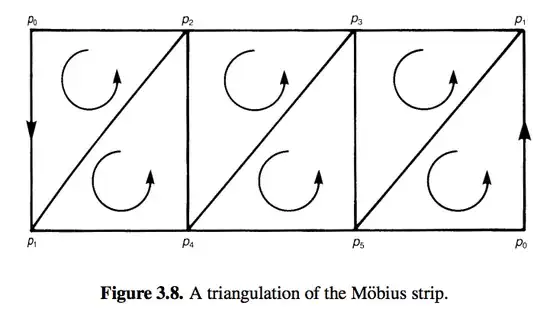
In the above diagram, we would like to say that the boundary of the entire strip consists of the edges $\langle p_1 p_3\rangle$, $\langle p_3 p_2\rangle$, $\langle p_2 p_0\rangle$, $\langle p_0 p_5\rangle$, $\langle p_5 p_4\rangle$, $\langle p_4 p_1\rangle$. Since the simplices are oriented by the order of their vertices, we could just say that this boundary is $$\langle p_1 p_3\rangle+\langle p_3 p_2\rangle+\langle p_2 p_0\rangle+\langle p_0 p_5\rangle+\langle p_5 p_4\rangle+\langle p_4 p_1\rangle$$ without ambiguity as to how the path is traversed, even if the order of these simplices were swapped.

Additionally (no pun intended), we would like to say that the total boundary of the strip is the sum of the boundary of the pieces. So when an edge is traversed one way in one piece and traversed the opposite way in another piece, as is the case with the edge $\langle p_1 p_2\rangle$ in $\langle p_0 p_1 p_2\rangle$ and $\langle p_1 p_4 p_2$, we could assign $\langle p_1 p_2\rangle$ from $\langle p_0 p_1 p_2\rangle$ with a positive sign, and the copy from $\langle p_1 p_4 p_2\rangle$ with a negative sign, so that when we take the boundary $\partial (\langle p_0 p_1 p_2\rangle+\langle p_1 p_4 p_2\rangle)$, the two terms (marked red) cancel, \begin{align} \partial (\langle p_0 p_1 p_2\rangle+\langle p_1 p_4 p_2\rangle) & = \partial \langle p_0 p_1 p_2\rangle+\partial\langle p_1 p_4 p_2\rangle\\ & = (\langle p_0 p_1\rangle + \color{red}{\langle p_1 p_2\rangle} - \langle p_0 p_2\rangle) + (\langle p_1 p_4\rangle - \langle p_2 p_4\rangle - \color{red}{\langle p_1 p_2\rangle} \\ & = \langle p_0 p_1\rangle - \langle p_0 p_2\rangle + \langle p_1 p_4\rangle - \langle p_2 p_4\rangle \end{align}

There are deeper reasons why taking free Abelian groups generated by not very algebraic looking objects is useful. At this stage I would suggest taking it on faith that you could "multiply a bunch of things by coefficients and add them up", just to see how the computation shakes out and how the results can be interpreted, then try to convince yourself that there is an intuition behind the exercise after all.

Elliot Yu
  • 2,350