Slopes and lines

Question

Given two lines having slope $m_1$ and $m_2$, the angle between them is given by $\tan(\theta)=\frac{m_2- m_1}{1+m_1m_2}$

Does the order of $m_1$ and $m_2$ matter here, and if so what is the significance? Graphical aid would be helpful.

Answer 1

Let's see what happens if we switch $m_1$ and $m_2$. First call $\theta_1$ an angle such that $\tan\theta_1 = \frac{m_2-m_1}{1+m_1m_2}$ and $\theta_2$ such that $\tan\theta_2 = \frac{m_1-m_2}{1+m_2m_1}$. Immediately you can see that $\tan\theta_1 = -\tan\theta_2$ and by tangens being odd function, we get $\tan\theta_1 = \tan(-\theta_2)$. If we restrict our $\theta$'s to $\langle-\pi/2,\pi/2\rangle$ (which we usually do in this case since we want the acute angle between lines) we get that $\theta_2 = -\theta_1$ so it is "the same" angle but measured in opposite directions (clockwise or counterclockwise).

In conclusion, $\theta_1$ is the angle between lines $l_1$ and $l_2$ measured from line $l_1$ to $l_2$ and $\theta_2$ is the angle between $l_1$ and $l_2$ measured from $l_2$ to $l_1$. They are of the same absolute value, but opposite orientations.

If you don't want to be bothered with orientation, you can change formula to $\tan\theta =\left|\frac{m_2-m_1}{1+m_1m_2}\right|$ and you will always get a positive angle and switching $m_1$ and $m_2$ won't change it since $|m_2-m_1|=|m_1-m_2|$.

Answer 2

Note that $m_1=\tan \theta_1$ and $m_1=\tan \theta_2$ are the tangents of the angles $\theta_1$ and $\theta_2$ between the lines and the $x$ axis. So: $$ \frac{m_2-m_1}{1+m_1m_2}=\frac{\tan \theta_2-\tan \theta_1}{1+\tan \theta_1\tan \theta_2}=\tan (\theta_2-\theta_1) $$ and: $$ \frac{m_1-m_2}{1+m_2m_1}=\frac{\tan \theta_1-\tan \theta_2}{1+\tan \theta_2\tan \theta_1}=\tan (\theta_1-\theta_2) $$ so the two formulas give two possible orientation for the angle $\theta$ between two lines.

Answer 3

Consider two non-perpendicular and non-vertical intersecting lines $\overleftrightarrow{l_1}$ and $\overleftrightarrow{l_2}$ in the coordinate plane.

Observe that $\overleftrightarrow{l_1}$ and $\overleftrightarrow{l_2}$ form two pairs of vertically opposite angles (acute angles $a$ and $c$, obtuse angles $b$ and $d$) between them.

To express $a$ and $b$ in terms of the slopes $m_1$ and $m_2$, let’s first see how they are related to the inclinations of $\overleftrightarrow{l_1}$ and $\overleftrightarrow{l_2}$, i.e. $p$ and $q$.

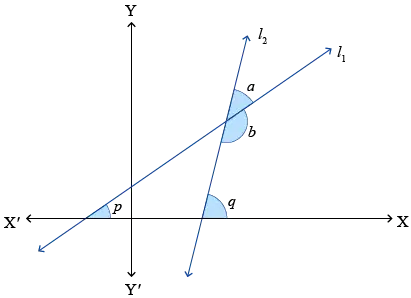
$$a=q-p$$ $$b= 180°-(q-p)$$

Now, since $p$ and $q$ are the inclinations of $\overleftrightarrow{l_1}$ and $\overleftrightarrow{l_2}$ respectively, their respective slopes are

$$m_1=\tan p$$ $$m_2=\tan q$$

So, to express a and b in terms of $m_1$ and $m_2$, let’s take the tan on both sides of (1) and (2) as follows: $$\tan a=\tan (q−p) and \tan b=\tan (180°−(q−p))$$ $$⇒ \tan a=\tan (q−p) and \tan b=−\tan (q−p)$$ [Using the result $\tan (180°−θ)=−\tan θ$.]

Using the above equations, we can express $\tan a and \tan b$ in terms of $m_1 and m_2$ as follows: $$ \begin{array}{l} \tan a=\dfrac{m_{2}-m_{1}}{1+m_{1} m_{2}} \\ \tan b=-\dfrac{m_{2}-m_{1}}{1+m_{1} m_{2}} \end{array} $$