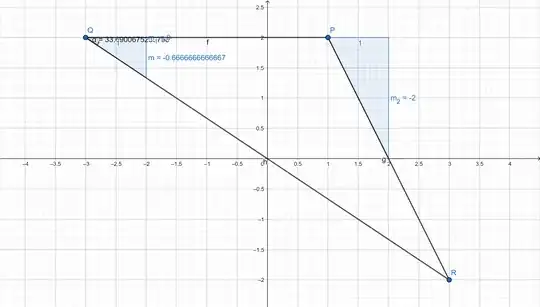
If $P(1,2)$, $Q(−3,2)$ and $R(3,−2)$ are the vertices of the triangle $PQR$, then find the value of $\tan Q$.
$\tan Q = 2/3$
I am unable to solve for $\tan Q$. I constructed the triangle $PQR$ and measured $\alpha$. I found $\tan Q$ to be $2/3$.
I am expected to solve it with slopes, but I am not limited to slopes. I found the slopes of $PQ, QR, \mathrm{and} PR$ i.e. $m_1$, $m_2$, $m_3$ respectively using:
\begin{aligned}m_{1}=\dfrac{2-2}{\left( -3\right) -1}=0\\ m_{2}=\dfrac{\left( -2\right) -2}{3-\left( -3\right) }=\dfrac{-2}{3}\\ m_{3}=\dfrac{\left( -2\right) -2}{3-1}=-2\end{aligned}