The angle between two lines of slope $m_1$ and $m_2$ is $$\tan \theta = \left|\dfrac{ m_1 - m_2}{1+m_1m_2} \right|$$
Now if $~\frac{ m_1 - m_2}{1+m_1m_2}~$ is positive then the angle between the lines is acute and if $~\frac{ m_1 - m_2}{1+m_1m_2}~$ is negative then the angle between the lines is obtuse.
Geometrically, the two different angles represent the same situation with respect to the lines.
For example if $~m_1 = 1/2~$ and $~m_2 = -1/3~,$ then $~\tan θ~$ comes out to be $~1~,$ which means $~θ = 45^\circ~.$ But if we take $~m_1= -1/3~$ and $~m_2= 1/2~,$ then $~\tan θ~$ would come out to be $~-1~,$ which means $~θ = 135^\circ~.$ For more understandable about the fact take a look at the next figure,
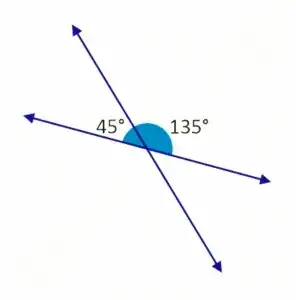
So, we needn’t worry about this issue much. But to keep things clean, we use a modulus sign on the formula of $~\tan\theta~$ i.e., the formula for the angle between two lines.
