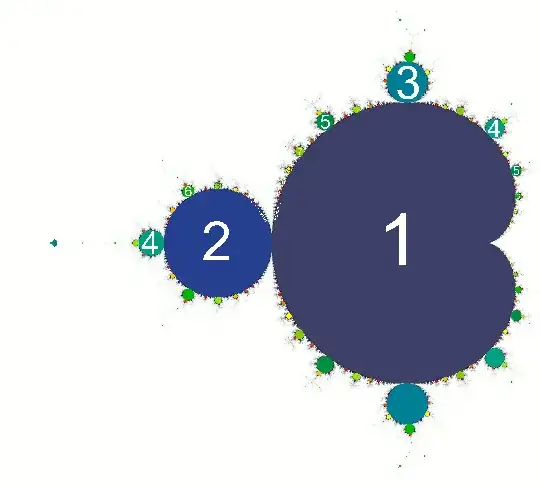
In the Mandelbrot Set, c=0 has a periodicity of 1 and is surrounded by a cartoid of non-periodic points that asymptotically approach periodicty 1. Extending left along the real axis are connected lobes of respective periodicity $2^1,2^2,2^3,2^4,2^5...$ Where exactly does that series of lobes end?
The center of the $2^8$-periodic lobe is -1.401153290849923, and there is a Misiurewicz Point (2-periodic after iteration 4) at -1.43036, so the end of the series of connected lobes must be somewhere between those two points.
The wiki article on Bifurcation Constants gives some detail on this $2^n$-periodic portion of the Mandelbrot but doesn't discuss the limit.
I am interested in the properties of this point more than a numerical estimate of its value. Is it transcendental, rational, a polynomial root, non-periodic, periodic, pre-periodic (Misiurewicz), a limiting case of pre-periodic?