How to draw a Mandelbrot Set with the connecting filaments visible?

Question

The M-Set is connected. But the M-Set viewers I’ve found create cool pictures that don’t really show the connecting filaments.

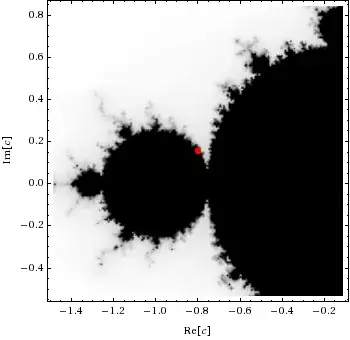
This mini-Mandel beetle should be connected to a larger min-Mandel by a black filament going into its “butt crack”, but you can’t see it here:

Monochrome pictures that show just the M-Set itself (not the colorful divergence contours) end up showing seemingly disconnected pieces where the filaments are still so thin they disappear between samples:

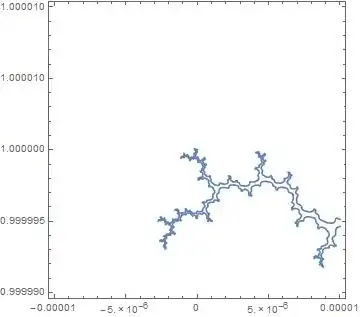
Denser sampling helps, but it’s very expensive, and pictures end up showing a lot of grey “fuzz” where the filaments become sub-pixel thin, so we still can't see how the mini-Mandels are connected.

I thought of using Mathematica to draw contour plots of $|z_n|==2$. For any given zoom level, there should be some high value of n for which the contour would be visually indistinguishable from the $z_\infty$ contour, right? I posted questions on the Mathematica SE site to get help on this approach, but using ContourPlot[] as a “zoom” function is tricky, though I haven't given up on this approach. My MMa-SE post on this approach is HERE

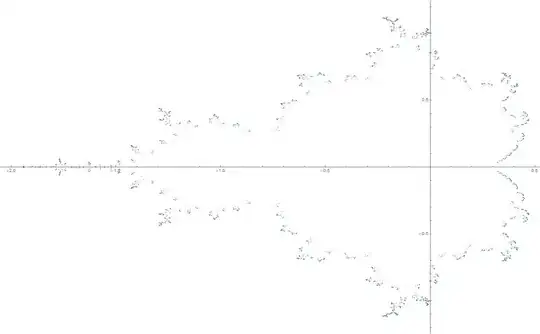
I also thought of calculating huge numbers of Misiurewicz Points which lie on the boundary of the Mandelbrot Set. Surely enough of them will make a picture, right? But this plot of 17,723 points was as far as this clever approach went before numerically solving $2^{16}$-order irreducible polynomials proved slightly impractical:

(If you like that picture, the MMa code to make it is on my question HERE)

So, does anyone have any other ideas for showing the filaments? Or fixes to my various failed ideas?

Answer 1

You want to colour the complement of the Mandelbrot set using the exterior distance estimate. For each pixel you calculate the running derivative (w.r.t. $c$) as well as the $z$ iterate, then at the end you combine them to get a distance estimate. Comparing this to the pixel spacing allows you to colour pixels close to the set black and pixels far from the set white. In practice I use $\tanh(d)$ (where $d$ is relative to pixel spacing) to give a smoother transition between white and black.

Pseudo-code (use a larger escape radius for finer appearance):

foreach pixel c
  while not escaped and iteration limit not reached
    dz := 2 * z * dz + 1
    z := z^2 + c
  de := 2 * |z| * log(|z|) / |dz|
  d := de / pixel_spacing
  plot_grey(tanh(d))

Your second image will look something more like this: