9

This relates to another challenge Question about drawing Mandelbrot filaments.

It is possible to compute a formula for a continuous path inside the Mandelbrot Set connecting $c=i$ to $c=0$? Obviously, the part inside the cartoid or lobes is easy, but finding any in-Set curve that includes $i$ has eluded me. I know the Mandebrot boundary is infinitely long and detailed, but if a filament has any finite thickness there should be a finite-length path through it that doesn't follow the boundary.

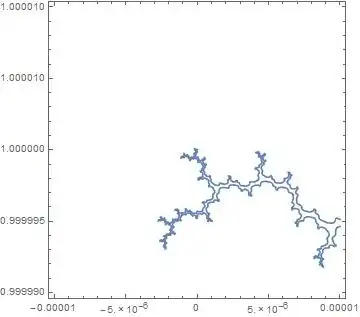
I tried to start by finding a direction one could travel from $i$ for a very short distance and remain in-Set, but even that eluded me.

To show the topology we're up against, here is the $|z_{25}|==2$ contour in the vicinity of i.

nearI

So, can one derive a formula for the path I want?

As an aside, it's worth noting that $i$ is a Misiurewicz Point, meaning its orbit is not immediately periodic but becomes so after a finite number of steps, i.e., $z_3(i)=z_1(i)$. This property places i exactly on the boundary of the Mandelbrot set.

$$i\rightarrow-1+i\rightarrow-i\rightarrow-1+i\rightarrow-i\rightarrow-1+i\rightarrow-i...$$

Community
  • 1
Jerry Guern
  • 2,764
  • The Hausdorff dimension of the boundary of $M$ is known to be $2$, so the path you are looking for may be infinite in length. Do we know that the filaments always have finite width? – Ross Millikan Jan 30 '16 at 16:12
  • @RossMillikan The path has points of infinitesimal width, probably an infinite number of them. This forces the path to go through all such points, but this alone does not force the path to have infinite length. – Jerry Guern Jan 30 '16 at 19:21

1 Answers1

4

Here's a zoom into the Mandelbrot set centered on $i$, with a factor of 10 magnification per frame. As you can extrapolate from the first frame, your path will have to go through an infinite number of bulbs before getting to any filaments. Then there will be an infinite number of tiny Mandelbrot islands to pass through, as they are dense in the filaments (they get very small very quickly). Finally you'll have to pass through an infinite number of 3-way Misiurewicz branch points, around which the Mandelbrot set is asymptotically self-similar.

All of this means I strongly doubt there is a simple formula for your desired path, if there is one at all. And if by "inside the Mandelbrot set" you mean "within the interior of the Mandelbrot set" then there is no such path possible, because you'll have to touch the boundary at the 3-way branching Misiurewicz points.

zoom into Mandelbrot set near $i$ (factor of 10 per frame)

PS: this image is rendered using exterior distance estimation, which I explained in my answer to your other question.

Claude
  • 5,852
  • Oh, I certainly wasn't expecting a "simple" formula. :-) Thank you for this well researched answer. It looks like the filament actually spirals infinitely many times around i. This means we can't even say what direction the connecting path extends from i, correct? I guess that property should have been obvious given self similarity, but I'd never thought about it explicitly before. – Jerry Guern Jan 30 '16 at 19:25
  • So, if someone asked, "What direction does the connecting path extend from i?" how would you explain that it doesn't? The set is connected, but there is no direction an ant at i can walk without stepping out of the set. – Jerry Guern Jan 30 '16 at 19:29
  • And by "inside the Set", I didn't mean interior, I included the boundary. What terminology should I have used? – Jerry Guern Jan 30 '16 at 19:31
  • I thnk you're right, but an ant walks in steps, so the direction could be described as a function of its leg length. Self-similarity means this function could be like a logarithmic spiral, if you let the ant have fat feet to fudge the wrinkles. Not sure about your terminology question, I'm not a topologist so maybe any perceived ambiguity was all my fault :) – Claude Jan 31 '16 at 01:14