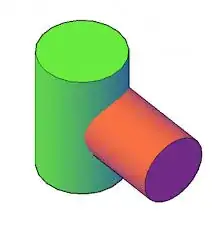
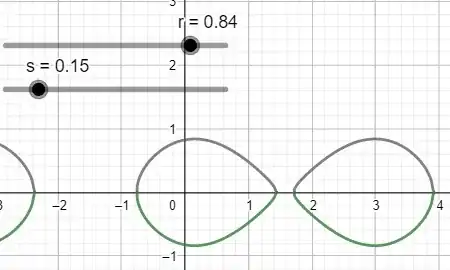A) Let us consider first the case of intersecting axes (even, as Jean-Claude Arbaut has pointed to, they aren't intersecting in the question). In fact, the equation of the unwrapped intersection curve is a general oval curve (see equation (*)) and even more complicated curves with equation (**) which are not ellipses.
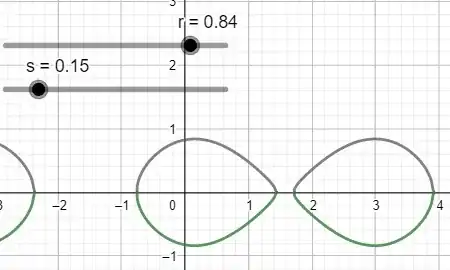
It is possible to play on the $r$ slider (and also the $s$ slider, see below) on the Geogebra figure:
https://www.geogebra.org/calculator/eugrnnec
(Look in particular how close to a circle is the curve when $r$ is small).
Its equation is (assuming the radius of the initial cylinder is $1$ and the boring cylinder has radius $r$ with the $x$ axis taken as its horizontal axis):
$$z=f_r(t)=r \sin(\cos^{-1}(\frac1r \sin(t)))\tag{*}$$
in a $(t,z)$ coordinate system .
Explanation:
$$\begin{cases}x&=&\cos(t)& \ Eq. 1a\\y&=&\sin(t)& \ Eq. 1b\end{cases}\tag{1}$$ and $$\begin{cases}y&=&r \cos(u)& \ Eq. 2a\\z&=&r\sin(u)& \ Eq. 2b\end{cases}\tag{2}$$
Indeed, knowing that unrolling the big cylinder is like taking angle $t$ as the new abscissa, it suffices to be able to express height $z$ as a function of $t$ as given by (*). This will be done in two steps, starting from the equality of Eq. 1b and Eq. 2b :
$$r\cos u= \sin t \implies u= \cos^{-1}(\frac1r \sin t),$$
and then plugging this expression into Eq. 2b.
B) Now, the non interesting case is a little more complicated because (2) has to be replaced by
$$\begin{cases}y&=&r \cos(u)+s& \ Eq. 2a\\z&=&r\sin(u)& \ Eq. 2b\end{cases}\tag{2}$$
where $s$ is the shift amount, finally giving:
$$z=f_{r,s}(t)=r \sin(\cos^{-1}(\frac1r (\sin(t)-s)))\tag{**}$$
Remark: Playing with the $s$ slider, you will see the interesting case of lemniscates (looking like an $\infty$ sign).