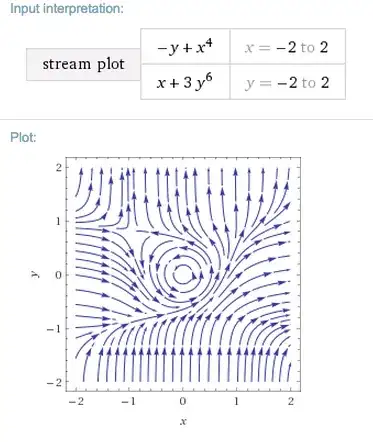
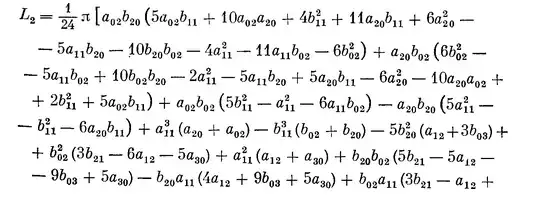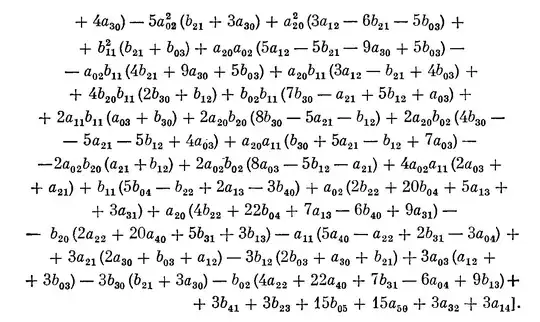The conjecture seems to be false. I write "seems" because still there is nonzero chance that I made a mistake in my calculation. However, I will present both numerical and analytical evidence for my conclusion.
First, analytically, to distinguish center from focus in a general situation one must compute the so-called Poincaré mapping that sends solutions starting at, say, polar angle $\theta=0$ and distance $r_0$ to $\theta=2\pi$. In general it has the form
$$
r=f(2\pi,0,r_0)=\alpha_1 r_0+\alpha_2 r_0^2+\alpha_3r_0^3+\ldots
$$
It is easy to compute $\alpha_1$ here, which is simply $\alpha_1=1$. Moreover, Lyapunov found that the first nonzero coefficient $\alpha_i$ with $i>1$, if any, must be such that $i$ is odd.
If one considers the function $f(2\pi,0,r_0)-r_0$, then this theorem is available, which I state following this book (Методы и приемы качественного исследованииа динамическикх систем на плоскости (Methods and techniques of the qualitative study of dynamical systems in the plane) – 1990,
by N. N Bautin, I am not aware of any English translation):
Theorem: If $\alpha_i\ne0$ for some $i>1$ odd then the equilibrium is a focus. If $\alpha_i=0$ for every $i>1$ odd then the equilibrium is a center.
So, this theorem is practically useless to prove that something is a center, but can be used to prove that the equilibrium is a focus. One calls $\alpha_3$ the first Lyapunov value (this is what is used in the Hopf bifurcation theorem) and $\alpha_5$ the second Lyapunov value.
Simple calculations show, as I mentioned in the comments, that $\alpha_3=0$. Furthermore, I found that
$$
\alpha_5=\frac{\pi}{12} \left(3a_2b_2(b_2^2-a_2^2)+11(a_2b_4-a_4 b_2)\right),
$$
where $a_j$ and $b_j$ are the coefficients of the Taylor series for $f$ and $g$ respectively, hence $\alpha_5\ne0$ in general. (More details on the computation of the coefficients $\alpha_i$ are in my second answer.)
So what about the StreamPlot function? It seems that, due to the fact that $\alpha_3=0$, the software does not distinguish between a center and a highly nonlinear focus (i.e., the convergence to the equilibrium is very far from being exponential).
So I took this system:
StreamPlot[{-y + x^2 + 2 x^4, x + y^2 + y^4}, {x, -1, 1}, {y, -1, 1}]
And got the expected picture of the center:
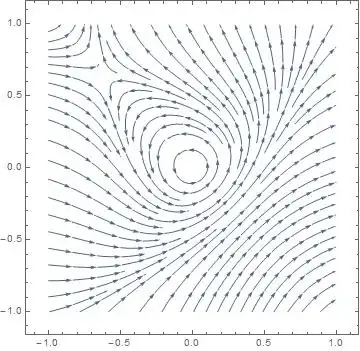
However, actually solving by Mathematica,
sol = {x[t], y[t]} /.
NDSolve[{x'[t] == -y[t] + x[t]^2 + 2 x[t]^4, y'[t] == x[t] + y[t]^2 + y[t]^4, x[0] == 1/5, y[0] == 1/5}, {x[t], y[t]}, {t, 0, 50}, AccuracyGoal -> 20, PrecisionGoal -> 20, WorkingPrecision -> 35];
ParametricPlot[Evaluate[sol], {t, 0, 50}]
I got the following figure:
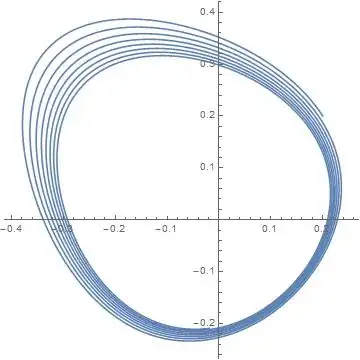
This confirms that the origin is a stable focus, as predicted by our computations that $\alpha_3=0$ and $\alpha_5=-\frac{11}{12}\pi<0$.