This is not a direct answer to the question, but a description of the real trajectories.
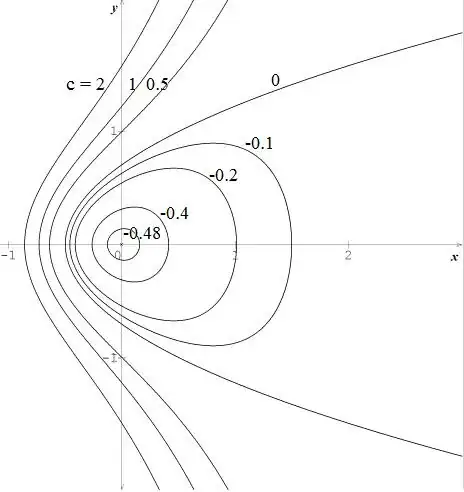
The limit case $c=-\frac{1}{2}$ is the point $(x=0\:,\:y=0)$ which is an isolated point. Losely, one can say that a trajectory reduced to an isolated point is at equilibrium.
If we displace slightly $(x,y)$ from $(0,0)$ to any position close to $(0,0)$ but not exactly on $(0,0)$ it comes on an almost circular trajectory and so, doesn't come back to the center. In this sense, the equilibrium point $(0,0)$ can be said "unstable".
Around $(0,0)$ (with $-\frac{1}{2}<c\ll 0$ ) the equation of trajectories is approximately :
$$y^2=(c+\frac{1}{2}) +(2c+1)x+(2c)x^2+O(x^3)$$
$$\left( \sqrt{-2c} \:x+x_0\right)^2+y^2=r^2+O(x^3)$$
where $x_0=\frac{c+\frac{1}{2}}{\sqrt{-2c} }$ and $r=\sqrt{ \frac{2c-1}{4c} (c+\frac{1}{2}) }$
The trajectory is an ellipse with center $(x_0\:,\:0)$ , with semiminor axis=$r$ and semimajor axis=$\frac{r}{\sqrt{-2c} }$.
The more $c$ is close to $-\frac{1}{2}$ , the more the trajectory is close to circular, with center close to $(0,0)$ and radius $r\simeq 0$ .