5

Consider the system of ODEs \begin{align*}x'&=y+x(\varepsilon+\ell_1(x^2+y^2)+\ell_2(x^4+y^4)) \\y'&=-x+y(\varepsilon+\ell_1(x^2+y^2)+\ell_2(x^4+y^4)).\end{align*}

Going through the linearization process at the equilibrium point $(0,0)$, we find the eigenvalues $\lambda_{1,2}(\varepsilon)=\varepsilon\pm i$. Using the Hopf Bifurcation theorem (p. 5-6), it is easy enough to show that a Andronov-Hopf Bifurcation appears when $\varepsilon=0$.

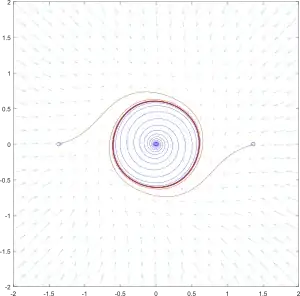
The issue is, if $\ell_1=0$, we fail to satisfy the conditions of the Hopf Bifurcation theorem, but a bifurcation still appears.

For example, suppose $\ell_1=0$ and $\ell_2=-1$. The following two images show our system for $\varepsilon=-0.1$ and $\varepsilon=0.1$, respectively.

enter image description hereenter image description here

So my first question is:

How would we show, analytically, that the system \begin{align*}x'&=y+x(\varepsilon+\ell_2(x^4+y^4)) \\y'&=-x+y(\varepsilon+\ell_2(x^4+y^4))\end{align*} has a Hopf Bifurcation at $\varepsilon=0$?

Secondly, if $\ell_1$ and $\ell_2$ have different signs, then we can have two limit cycles, depending on $\varepsilon$. For example, suppose $\ell_1=1$ and $\ell_2=-1$. The next two images show when $\varepsilon=0.1$ and $\varepsilon=-0.1$, respectively.

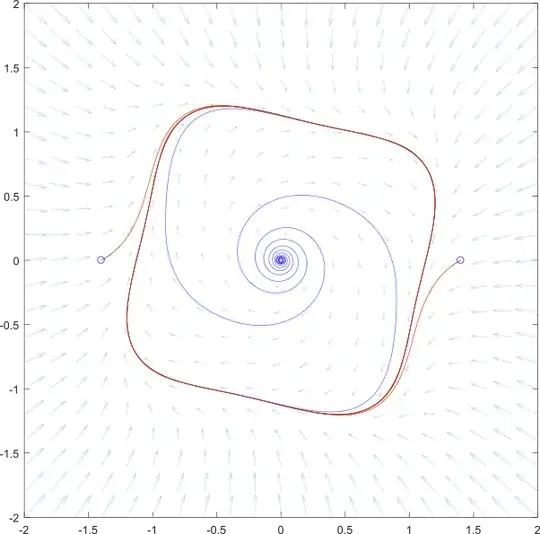
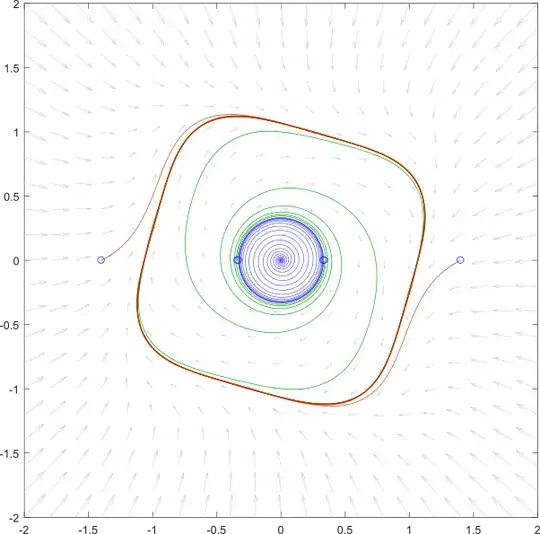
Now, these two limit cycles will eventually collapse on each other as $\varepsilon$ decreases, but otherwise, there is always at least one limit cycle. So my second question is:

How would we show, analytically, that the system \begin{align*}x'&=y+x(\varepsilon+(x^2+y^2)-(x^4+y^4)) \\y'&=-x+y(\varepsilon+(x^2+y^2)-(x^4+y^4)) \end{align*} has a single limit cycle for all $\varepsilon>0$?

Bonnaduck
  • 4,178

1 Answers1

1

The short answer to your questions is "by calculating the second Lyapunov value", and if it is also zero then the third one and so on... Details, explanations and references can be found in two my answers here.

Community
  • 1
Artem
  • 14,847
  • Just to make sure I understand. I found that $\frac{dr}{d\theta}=-\varepsilon r-\ell_1r^3-\ell_2(\cos^4\theta+\sin^4\theta)r^5$. Does this immediately imply that the second and third terms are my first and second Lyapunov values? – Bonnaduck Mar 19 '17 at 20:48
  • No, it does not. – Artem Mar 19 '17 at 21:09
  • Okay. So, using the notation you used, I have $R_1(\theta)=-\varepsilon$, $R_3(\theta)=-\ell_1$, and $R_5(\theta)=-\ell_2(\cos^4(\theta)+\sin^4(\theta))$, with $R_i(\theta)=0$ for all other $i$. I am still confused on how you proceed from here. I get equating $u'_1(\theta)=R_1(\theta)u_1$, etc., but after that I am a bit lost. – Bonnaduck Mar 20 '17 at 00:39