For a graph $G$, let $W$ be the (random) vertex occupied at the first time the random walk has visited every vertex. That is, $W$ is the last new vertex to be visited by the random walk. Prove the following remarkable fact:
For the random walk on an $n$-cycle, $W$ is uniformly distributed over all vertices different from the starting vertex.
Consider a simple symmetric random walk on the integer line starting from $0$ and, for some integers $-a\leqslant 0\leqslant b$ such that $(a,b)\ne(0,0)$, the event that the walk visits every vertex in $[-a,b]$ before visiting vertex $-a-1$ or vertex $b+1$. This is the disjoint union of two events:
Recall that the probability that a simple symmetric random walk starting from $i$ visits $i-j\leqslant i$ before visiting $i+k\geqslant i$ is $\frac{k}{k+j}$, for every nonnegative integers $j$ and $k$.
Hence, the probability of Event 1 is $\frac{a}{a+b}\cdot\frac1{a+b+1}$, the probability of Event 2 is $\frac{b}{a+b}\cdot\frac1{a+b+1}$, and the probability of their union is $\frac1{a+b+1}$. Note that this last formula is also valid when $a=b=0$.
If $b=x-1$ and $a=n-x-1$ with $1\leqslant x\leqslant n-1$ and $n\geqslant2$, then $a+b+1=n-1$ hence the computation above shows that the probability that the last visited vertex in the discrete circle $\{0,1,\ldots,n-1\}$ is $x$ is $\frac1{a+b+1}=\frac1{n-1}$. That is, the probability of the event $[W=x]$ is $\frac1{n-1}$ for each $x\ne0$ in the circle, and $W$ is uniformly distributed on the circle minus the starting point of the random walk.
This question is rephrased as a game and can be analyzed with no computation!
A class of 30 children is playing a game where they all stand in a circle along with their teacher. The teacher is holding two things: a coin and a potato. The game progresses like this: The teacher tosses the coin. Whoever holds the potato passes it to the left if the coin comes up heads and to the right if the coin comes up tails. The game ends when every child except one has held the potato, and the one who hasn't is declared the winner.
How do a child's chances of winning change depending on where they are in the circle? In other words, what is each child's win probability?
It is equivalent to show that all students have equal probability of winning. To this end, consider the students to the left and the right of the teacher. Call them the teacher's pets. Both teacher's pets have equal probability of winning by symmetry.
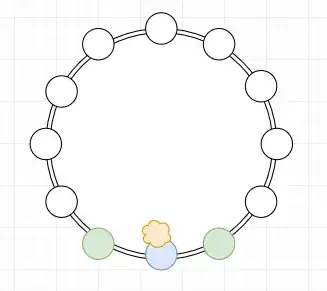
Diagram 1: The teacher is blue, the teacher's pets are green, and the potato is a lumpy yellow cloud. Small white circles are the other students.
Now consider any student who hasn't lost yet. We can show he has the same chance of winning as a teacher's pet. Call this student "Purple".
Diagram 2: Purple is a student who hasn't lost yet.
With $100 \%$ certainty, the potato will arrive to Purple's left or to his right eventually. Consider the first time this happens.
Diagram 3: The potato touches one of his neighbors for the first time. Red players have lost already.
In that situation, he use the power of imagination! He can image that he himself is a teacher's pet since his situation has become identical to the starting condition, and therefore his probability of winning is the same as that of the teacher's pets.
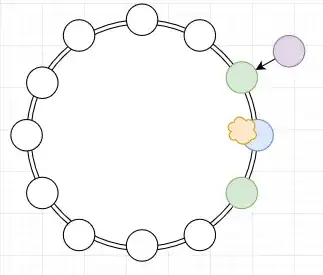
Diagram 4: Purple imagines that he is a teacher's pet. The arrow should be understood to mean "imagines himself as".
The right-hand neighbor is in immediate danger of losing if the ball happens to travel counter-clockwise through the purple player.
– Mark Jan 04 '20 at 20:34In order to reach $W$ last, the walk has to visit one of $W$'s neighbours for the last time and then go all around the cycle to arrive at $W$ from the other side. Let's call a segment of a random walk on the cycle that starts at some vertex $V$ and reaches one of $V$'s neighbours by going around the cycle without returning to $V$ a final segment. Then the last vertex reached after time $t$ is the final vertex of the first final segment that begins at or after $t$. Consider a random walk on the cycle, and for every final segment that ends at $W$, consider the stretch of times $t$ for which it is the first final segment that begins at or after $t$. If we can show that all vertices except $W$ occur with the same frequency in this stretch, then it will follow that conversely $W$ is reached last with the same probability from all other vertices, and thus all vertices $W$ are reached last with the same probability from a given initial vertex.
But the stretch extends precisely up to the last visit to $W$ before the segment, so the frequency of vertices in it is just that between any two successive visits to $W$, which is just the frequency of occurrence of the vertices other than $W$ in the walk in general, which is the same for all vertices.
P.S.: It's actually not too difficult to determine the probability of each vertex to be the last vertex visited at any stage in the process. The vertices already visited always form an interval. If the current position is at the end of an interval of $k$ visited vertices, every unvisited vertex has the same $1/(n-1)$ probability of becoming the last one, except the first unvisited vertex at the other end of the interval, which has $k/(n-1)$. This is because for all vertices except this one, exactly the same realizations of the walk will make them the last vertex as would be the case if no vertices had been visited yet. Thus, every vertex has a constant probability $1/(n-1)$ of ending up as the last vertex until the walk first visits one of its neighbours.
If the current position is in the interior of the interval of visited vertices, the probability of reaching one end of the interval before the other varies linearly over the interval, and thus so do the probabilities of the two unvisited vertices bordering the interval to become the last vertex – the sum of their probabilities is $(k+1)/(n-1)$, and this shifts by $1/(n-1)$ by each move, in favour of the vertex that the move moves away from.
A: A easier question is with a simple random walk (no circle), the probability of hitting $+a$ before $-b$ is $\frac{b}{a+b}$ and of hitting $-b$ before $+a$ is $\frac{a}{a+b}$. (To see this, consider that expected position when you stop having hit one of them is always $0$ as this is a martingale.)
B: In the circle walk, for the vertex immediately clockwise from the starting vertex, it is the last to be visited if in A you visit $-(n-2)$ before $+1$, which has probability $\frac{1}{n-1}$. Similarly for the vertex immediately anti-clockwise from the starting vertex.
C: For a vertex $k$ steps clockwise from the starting vertex (i.e. $-(n-k)$ anticlockwise) to be the last to be visited, either you hit $k-1$ before $-(n-k-1)$ with probability $\frac{n-k-1}{n-2}$ as in $A$ and then reverse almost all the way round as in B with probability $\frac{1}{n-1}$, or you hit $-(n-k-1)$ before $k-1$ with probability $\frac{k-1}{n-2}$ and then reverse almost all the way round with probability $\frac{1}{n-1}$. So combining these, the probability is $$\frac{n-k-1}{n-2}\frac{1}{n-1}+\frac{k-1}{n-2}\frac{1}{n-1}=\frac{1}{n-1}$$ and this does not depend on the value of $k$.
Mark's no-calculation solution short-cuts C (and indeed B and A) by saying that for a given point, one of its neighbours will be inevitably be visited before the other neighbour and before the given point is; from there, for the given point to be visited last, you then need to visit the other neighbour going back round before visiting the given point, with the probability of that second event being the same for all possible given points based on the symmetry.
