Continuing the discussion with Alan (see his answer above) I would like to present the approach here for the computation of the cover time. I am basically following the ideas of Lovász [Lov93] as presented in "Markov Chains and Mixing Times", Levin et al, Chapter 11, Example 11.1 along with the formula we will derive at the end.
If we have a symmetric Random Walk $(X_n)_{n\geq0}$ on $\mathbb Z/n$ (cycle graph), where $n\geq 1$, we can ask for the expected time to visit all the $n$ states at least once. The counting stops when we reach the last new state for the first time. Let us call this time $\tau^n_{cov}$ (cover time).
Further we can assume that we start with probability $1$ in some given state. Then the RW visits a new state in the next step, as we can not stay where we began. We then have two options: either we leave this set of two already visited states to left or to the right. For example, if we started in 0, and the next state was 1, we either go directly to the new state 2, or we travel via 0 to n-1.
Directly after, we again wait until the RW has left the set of now three states at either end. And so on.
This is the classic situation of computing the number of games before a gambler either is ruined or beats the opponent. We call this ruin time $\tau^{(r,n)}$.
For that we can use first-step-analysis. Let $f_n(k):=\mathbb E(\tau^{(r,n)}|Z_0=k)$.
We can now think of a state space $\{0,1,2,\ldots,n\}$, where $n$ and $0$ are absorbing.
We get:
$$f_n(0)=0$$
$$f_n(1)=1+\frac12f_n(0)+\frac12f_n(2)=1+\frac12f_n(2)$$
$$...$$
$$f_n(k)=1+\frac12f_n(k-1)+\frac12f_n(k+1)$$
$$...$$
$$f_n(n)=0$$
Like in the answer by Allan, we assume that $f_n(k)$ is a quadratic polynomial, such that $f_n(k)=a\cdot k^2+b\cdot k+c$ with real numbers $a,b,c$ yet unknown.
Using $f_n(0)=0$ we get immediately $c=0$. After this reduction we just need to solve the system of equations above for general $k, 1\leq k\leq n-1$:
$$ak^2+bk=1+\frac12(k-1)(a(k-1)+b)+\frac12(k+1)(a(k-1)+b)=1+a(k^2+1)+bk$$
Luckily this reduces after some simple algebra to just $a=-1$.
Now we have $f_n(k)=-k^2+bk$ and need to find the value of $b$. For that, we use the case for $k=n$, which gives:
$$f_n(n)=-n^2+bn=0\Leftrightarrow b=n$$
Finally, we have found $f_n(k)=-k^2+nk=(n-k)k$. Indeed, we actually need to evaluate the function only at $k=1$ or equivalently at $n-1$, as we always start at the boundary.
Now we can combine both results. If we have in total n states in the cycle graph:
$$\mathbb E[\tau^n_{cov}]=\sum_{i=2}^{n}f_i(1)=\sum_{i=2}^{n}(i-1)1=\sum_{i=1}^{n-1}i=\frac12n(n-1)$$
Either way, for the original question, we get exactly $\mathbb E[\tau_{cov}]=1+2+3+4=\frac125*4=10$.
Since all the states except the first one, are equally likely to be the last, the number of steps to reach 3 takes on average 10 steps, unless of course we had started in 3.
A simulation confirms that. All states exept the first one are equally likely to be the last. A histogramm confirms the uniform distribution over all non-starting states.
With 100000 samples I got an estimate of 9.97144 for the cover time and this for the distribution on the end states: [0.24762, 0.25162, 0.2512, 0.24956]
[Lov93] On the last new vertex visited by a random walk, Lovász and Winkler, Journal of Graph Theory 17, p 593-596
If needed the code i used in Processing (JAVA)
ArrayList<Integer> visitedStates = new ArrayList<Integer>();
int firstState;
int currentState;
int expSteps=0;
float sum = 0;
float samples = 100000;
int[] hist = new int[4];
for(int i = 0; i < samples; i++) {
visitedStates.clear(); firstState = 1;
currentState = firstState;
expSteps = 0;
visitedStates.add(firstState);
while(visitedStates.size() != 5) {
float theta = random(0,1);
if(theta > 0.5) {
currentState += 1;
}
else {
currentState -= 1;
}
if(currentState<1) { currentState = 5; }
if(currentState>5) { currentState = 1; }
if(!visitedStates.contains(currentState)) {
visitedStates.add(currentState);
}
expSteps++;
}
hist[currentState-2] += 1;
sum += expSteps;
}
println(sum/samples);
println(hist[0]/samples +", " + hist[1]/samples
+", " + hist[2]/samples + ", " + hist[3]/samples);
Some extra notes:
With some adaptions, we can also see what the expected number of steps until cover with respect to some given end state is.
For that we something more. Assuming, we start in state 1 we either go to {1,2} which is neighbouring 3. Therefore we have to leave that subset via 1 to 5. The other case is {1,5}, then it is not important to which other state we go next, as both are not 3.
The complete case study is displayed in the image. Red subsets are neighbouring 3 only on one side.
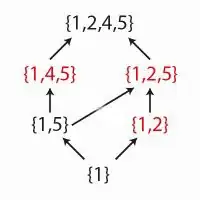
We therefore need to compute the average number of games in a symmetric gambler's ruin chain if condition the process to ruin in the end. We assume again a state space of the natural numbers from 0 to some fixed n. In this situation 0 and n are absorbing.
Let $\tau_R$ be the (stopping) time until ruin (time to reach 0). We know that the event $\{\tau_R<\infty\}$ is equivalent to the event of ruin at some point in the future.
For given $i,j\in\{1,\ldots,n-1\}$ we can compute the following conditional probability: $\mathbb P(X_n=j| \tau_R<\infty, X_0=i)$.
In this form it is not very handy, but we can simplify the expression:
$$\mathbb P(X_n=j|\tau_R<\infty,X_0=i)=\frac{\mathbb P(\exists m\geq0:X_{n+m}=0|X_n=j)}{\mathbb P(\exists m'\geq0:X_{n+m'}=0|X_n=i)}\cdot\mathbb P(X_n=j|X_0=i)$$
$$=\frac{\mathbb P(\tau_R<\infty|X_0=j)}{\mathbb P(\tau_R<\infty|X_0=i)}\mathbb P(X_n=j|X_0=i)$$
The ratio of probabilities is actually known, as these are just the ruin probabilities that Alan computed. Therefore
$$\mathbb P(\tau_R<\infty|X_0=k)=1-\frac kn$$
and therefore
$$\mathbb P(X_n=j|\tau_R<\infty,X_0=i)=\frac{n-j}{n-i}\mathbb P(X_n=j|X_0=i).$$
In particular, if we assume time homogeneity (as we did in the previous computation), we also get for a single step:
$$\mathbb P(X_1=j|\tau_R<\infty,X_0=i)=\frac{n-j}{2(n-i)}.$$
This transforms the problem now into a simple absorption problem. Note, the probability to go from state n-1 to n is now zero. Naturally, one could swap the roles of 0 and n, as everything is symmetric.
To compute the average absorption time we simply follow the same approach as before using first step analysis. Let $g(i)=\mathbb E[\tau|X_0=i]$ where $\tau$ is now the absorption time in the new system.
$$g(0) = 0$$
$$g(k)=1+ \frac{n-k+1}{n-k}g(k-1)+\frac{n-k-1}{n-k}g(k+1)$$
$$g(n-1)=1+g(n-2)$$
The last equation states that we have to go to n-2 if we are in n-1, as now going to n is not allowed anymore. I have not bothered to find the general solution to this.
In any case, we just need to solve this for $n=3$ and $n=4$. Escaping to 0 in the first case is on average 8/3 if started in n-1, and in the second case we get 5.
Now we just need to notice that in the above diagram the transition from one set to another are determined just by either the probability to leave or to leave at one side starting at a boundary state.
