0

Here is a problem. Could everybody help me, please, or just send a link, to the solution. One evening, a playful host hosts us for dinner, who a at the end of dinner, you want to raffle a gift among the guests. At the start of the game, the guests and the host, with the gift in hand, sit around a round table. The host rolls one in the case of regular coins and heads, he passes the box to his right neighbor, while in the case of a write, he passes the box to his left neighbor. The guests also repeat this process, until someone receives the box first, so that it was already in the hands of every other guest, then he is the winner of the gift. What is the expected value of the gametime? How is it possible to calculate? I know that the game is fair, that is, no matter where we sit, we always have a $1/n$ chance of winning, where $n$ is the number of players. I did a simulation in R to guess the expected value, but I can't conclude anything from it, unfortunately...:( Thanks the answers, and I would like to know that ss there any result about how $T_N$ is distributed, so what is the distribution of $T_N$ , where $T_N$ is the time, when the process stop, and $N$ is the number of guests? It is possiblbe approx with something normal?! This picture shows the T15 results, if I simulated 10000 times. On the $x$-axis you can see the number of steps, and ond the $y$ axis the frequency. 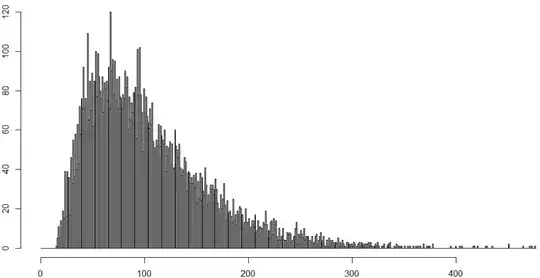enter image description here

Elemer Kit
  • 83
  • Just for reference: The question of why everybody has equal probability of winning has been discussed here https://math.stackexchange.com/questions/116446/random-walk-on-n-cycle. – DominikS Oct 01 '23 at 11:07
  • This might answer your question: https://math.stackexchange.com/questions/1445154/step-in-computation-of-the-expected-cover-time-for-the-simple-random-walk-on-a-d – DominikS Oct 01 '23 at 11:12
  • Thanks a lot, it will be help :) Is there any result about how $T_N$ is distributed, so what is the distribution of $T_N$, where $T_N$ is the time, when the process stop, and $N$ is the number of guests? It is possiblbe approx with something normal?! – Elemer Kit Oct 01 '23 at 19:57

0 Answers0