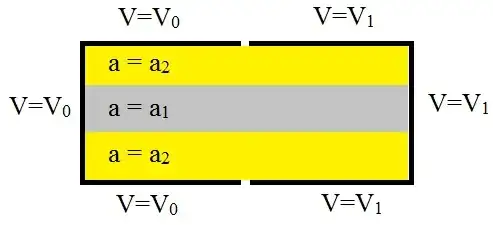
A numerical solution of the Laplace equation (in a rectangular geometry)
can be obtained with an equivalent resistor network.
Key internet references are found here:
In our case, the domain of interest in subdivided in rectangles:
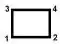
Let the width and height of a rectangle be given by $\,dx\,$ and $\,dy\,$
respectively,
then each of the four edges is associated with a resistor $\,R\,$ having
admittance $\,A_x = \lambda/dx\cdot dy/2\,$ for the horizontal edges and
$\,A_y = \lambda/dy\cdot dx/2\,$ for the vertical edges, where $\lambda$
is the conductivity (equal to $a_1$ or $a_2$ in the OP's question).
Resulting in the following "Finite Element matrix" for one rectangle:
$$
\begin{bmatrix} A_x+A_y & - A_x & - A_y & 0 \\
- A_x & A_x+A_y & 0 & - A_y \\
- A_y & 0 & A_x+A_y & - A_x \\
0 & - A_y & - A_x & A_x+A_y \end{bmatrix}
$$
The rest of the numerical treatment is pretty standard Finite Element
methodology:
program hesam;
Uses Laplace;
procedure test;
var
k : integer;
begin
Starten; {Initialize }
for k := 0 to 9 do
begin
{ FEM Calculations }
Rekenen(Random,Random,0,1);
{ Store in 'results' file }
Opschrijven(k);
end;
end;
begin
test;
end.
Here is a link to the complete (Delphi Pascal) unit that
does the FEM Calculations:
Below is the $\,40\times 30\,$ grid that has been used for sample
calculations and a contour map of some results with $V_0=0$ ,
$V_1=1$ and random $a_1,a_2$.

Sample output ('result' file) - can you see where it is? - :
x y V[x,y]
20 0 5.00000000000000E-0001
20 1 5.00000000000000E-0001
20 2 5.00000000000000E-0001
20 3 4.99999999999999E-0001
20 4 4.99999999999999E-0001
20 5 4.99999999999999E-0001
20 6 4.99999999999999E-0001
20 7 4.99999999999999E-0001
20 8 4.99999999999999E-0001
20 9 5.00000000000000E-0001
20 10 5.00000000000001E-0001
20 11 5.00000000000001E-0001
20 12 5.00000000000001E-0001
20 13 5.00000000000002E-0001
20 14 5.00000000000002E-0001
20 15 5.00000000000002E-0001
20 16 5.00000000000003E-0001
20 17 5.00000000000003E-0001
20 18 5.00000000000003E-0001
20 19 5.00000000000002E-0001
20 20 5.00000000000002E-0001
20 21 5.00000000000003E-0001
20 22 5.00000000000002E-0001
20 23 5.00000000000002E-0001
20 24 5.00000000000001E-0001
20 25 5.00000000000001E-0001
20 26 5.00000000000001E-0001
20 27 5.00000000000001E-0001
20 28 5.00000000000000E-0001
20 29 5.00000000000000E-0001
20 30 5.00000000000000E-0001