How does one implement Hadamard gate in Pauli-based computation?

Question

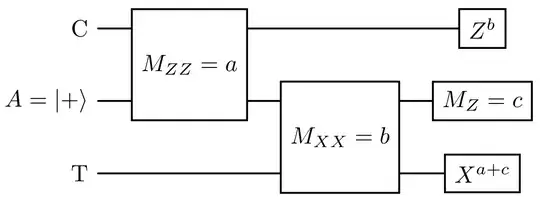
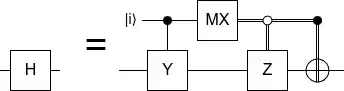
Pauli-based computation supposedly gives the full Clifford group.

For instance, the CNOT can be implemented using joint ZZ measurement and joint XX measurement and using an additional ancilla qubit.

To generate the Clifford group, it would be sufficient to have similar gadgets for S and H. How does one achieve a hadamard gate just using measurements?

(This is a question at the logical level - not asking about specifics of any code. Although, surface code lattice surgery examples could still help.)

Craig Gidney · Answer 1 · 2025-04-25T04:51:21.027

Stim's gate set documentation includes MBQC decompositions of every gate.

Assuming the gateset is MX, MY, MZ, MXX, MZZ, and Pauli feedback:

import stim
assert stim.Circuit("""
    MY 1
    MZZ 0 1
    MX 1
    # Classical feedback.
    CZ rec[-1] 0
    CZ rec[-2] 0 
    CZ rec[-3] 0
""").has_all_flows(stim.gate_data('S').flows)
assert stim.Circuit("""
    MX 1
    MZZ 0 1
    MY 1
    MXX 0 1
    MZ 1
    MX 1
    MZZ 0 1
    MY 1
    # Classical feedback.
    CZ rec[-1] 0
    CZ rec[-2] 0
    CZ rec[-3] 0
    CY rec[-4] 0
    CY rec[-5] 0
    CZ rec[-6] 0
    CX rec[-7] 0
    CX rec[-8] 0
""").has_all_flows(stim.gate_data('H').flows)

score 5 · Answer 2 · answered Apr 24 '25 at 06:30

In general, you would achieve similar features for $S$ and $H$ by using some form of teleportation.

Assuming you refer to something similar to the following figure:

This type of teleportation process requires resource states. In the case of $CNOT$, it requires a $|+\rangle$ state. You can do something similar for $H$ in a single qubit teleportation at the logical level:

How does one implement Hadamard gate in Pauli-based computation?

2 Answers2