3

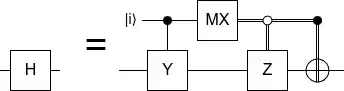
The circuit in Figure 13.7 of Gottesman's book https://www.cs.umd.edu/class/spring2024/cmsc858G/QECCbook-2024-ch1-15.pdf shows how to take the magic state $ T | + \rangle $ and use single bit gate teleportation to implement the $ T $ gate on a qubit $ | \psi \rangle $.

The state $ H | + \rangle= | 0 \rangle $ doesn't do anything useful. Is there some other state that we can use, with controlled Paulis and computational basis measurements, to implement a Hadamard gate on $ | \psi \rangle $ through single bit gate teleportation?

Ian Gershon Teixeira
  • 5,358
  • 6
  • 30

1 Answers1

5

Here's a construction that does it with a one qubit state, by using a CY gate and an MX gate. This works because Hadamard is, up to Pauli gates, equivalent to a 90 degree rotation around the Y axis.

enter image description here

Craig Gidney
  • 47,099
  • 1
  • 44
  • 119