Does a T gate via teleportation use 1 magic state for $n$ T gates or $n$ magic states for $n$ T gates?

Question

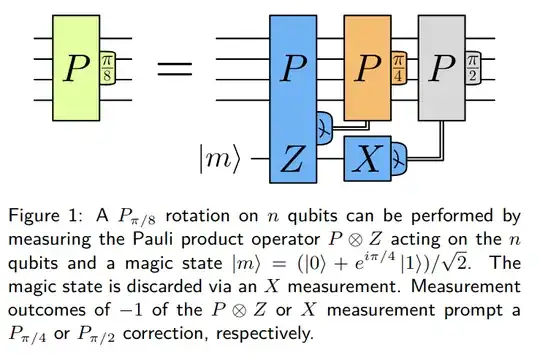
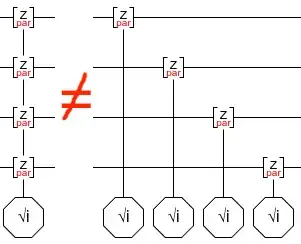
In Magic State Distillation: Not as Costly as You Think,

Shows that a $P_\frac{\pi}{8}$ gate can per done on $n$ qubits using 1 magic state. When I simulate this circuit though, it doesn't seem to provide the correct output.

I first start by simulating an X gate using T gates without any teleportation 100 times

0: ───H───T───T───T───T───H───M───

This gives the right result: {1: 100}

I then do the same as the above but implement the first T gate with teleportation

                     ┌─────┐
0: ───H───────M(Z)────S────────Z───T───T───T───H───M───
              ║       ║        ║
1: ───H───T───M(Z)────╫M(X)────╫───────────────────────
              ║       ║║       ║
a: ═══════════@═══════^╬═══════╬═══════════════════════
                       ║       ║
b: ════════════════════@═══════^═══════════════════════

We get the same counts as the first circuit. Looking good so far.

We then simulate the circuit from Figure 1 of the "Not as Costly as you think paper"

                     ┌────────┐   ┌────┐
0: ───H───────M(Z)────S────────────Z───────T───T───T───H───M───
              ║       ║            ║
1: ───H───────M(Z)────╫S───────────╫Z──────T───T───T───H───M───
              ║       ║║           ║║
2: ───H───────M(Z)────╫╫S──────────╫╫Z─────T───T───T───H───M───
              ║       ║║║          ║║║
3: ───H───────M(Z)────╫╫╫S─────────╫╫╫Z────T───T───T───H───M───
              ║       ║║║║         ║║║║
4: ───H───T───M(Z)────╫╫╫╫M(X)─────╫╫╫╫────────────────────────
              ║       ║║║║║        ║║║║
a: ═══════════@═══════^^^^╬════════╬╬╬╬════════════════════════
                          ║        ║║║║
b: ═══════════════════════@════════^^^^════════════════════════
                     └────────┘   └────┘

This one does not give the same counts, which makes me suspect that the T gate is not being implemented correctly.

We then use a magic state for each T gate we want to implement

              ┌────────────────┐   ┌────────────────────┐   ┌────┐
0: ───H────────M(Z)─────────────────S────────────────────────Z───────T───T───T───H───M───
               ║                    ║                        ║
1: ───H────────╫───M(Z)─────────────╫S───────────────────────╫Z──────T───T───T───H───M───
               ║   ║                ║║                       ║║
2: ───H────────╫───╫───M(Z)─────────╫╫S──────────────────────╫╫Z─────T───T───T───H───M───
               ║   ║   ║            ║║║                      ║║║
3: ───H────────╫───╫───╫───M(Z)─────╫╫╫S─────────────────────╫╫╫Z────T───T───T───H───M───
               ║   ║   ║   ║        ║║║║                     ║║║║
4: ───H───T────M(Z)╫───╫───╫────────╫╫╫╫M(X)─────────────────╫╫╫╫────────────────────────
               ║   ║   ║   ║        ║║║║║                    ║║║║
5: ───H───T────╫───M(Z)╫───╫────────╫╫╫╫╫───M(X)─────────────╫╫╫╫────────────────────────
               ║   ║   ║   ║        ║║║║║   ║                ║║║║
6: ───H───T────╫───╫───M(Z)╫────────╫╫╫╫╫───╫───M(X)─────────╫╫╫╫────────────────────────
               ║   ║   ║   ║        ║║║║║   ║   ║            ║║║║
7: ───H───T────╫───╫───╫───M(Z)─────╫╫╫╫╫───╫───╫───M(X)─────╫╫╫╫────────────────────────
               ║   ║   ║   ║        ║║║║║   ║   ║   ║        ║║║║
a: ════════════@═══╬═══╬═══╬════════^╬╬╬╬═══╬═══╬═══╬════════╬╬╬╬════════════════════════
                   ║   ║   ║         ║║║║   ║   ║   ║        ║║║║
b: ════════════════@═══╬═══╬═════════^╬╬╬═══╬═══╬═══╬════════╬╬╬╬════════════════════════
                       ║   ║          ║║║   ║   ║   ║        ║║║║
c: ════════════════════@═══╬══════════^╬╬═══╬═══╬═══╬════════╬╬╬╬════════════════════════
                           ║           ║║   ║   ║   ║        ║║║║
d: ════════════════════════@═══════════^╬═══╬═══╬═══╬════════╬╬╬╬════════════════════════
                                        ║   ║   ║   ║        ║║║║
e: ═════════════════════════════════════@═══╬═══╬═══╬════════^╬╬╬════════════════════════
                                            ║   ║   ║         ║║║
f: ═════════════════════════════════════════@═══╬═══╬═════════^╬╬════════════════════════
                                                ║   ║          ║║
g: ═════════════════════════════════════════════@═══╬══════════^╬════════════════════════
                                                    ║           ║
h: ═════════════════════════════════════════════════@═══════════^════════════════════════
              └────────────────┘   └────────────────────┘   └────┘

This one works as it should.

What's going on? Am I reading gate teleporation figures incorrectly again?

I've pasted the code used to generate these circuits below to aid in reproduction of the results.

import collections
import cirq
def x_gate_on_1_qubit():
    return cirq.Circuit(
        cirq.H(cirq.q(0)),
        cirq.T(cirq.q(0)),
        cirq.T(cirq.q(0)),
        cirq.T(cirq.q(0)),
        cirq.T(cirq.q(0)),
        cirq.H(cirq.q(0)),
        cirq.measure(cirq.q(0)),
    )
def gate_teleportation_on_1_qubit():
    return cirq.Circuit(
        cirq.H.on_each(cirq.q(0), cirq.q(1)),
        cirq.T(cirq.q(1)),
        cirq.measure_single_paulistring(cirq.Z(cirq.q(0)) * cirq.Z(cirq.q(1)), key="a"),
        cirq.S(cirq.q(0)).with_classical_controls("a"),
        cirq.measure_single_paulistring(cirq.X(cirq.q(1)), key="b"),
        cirq.Z(cirq.q(0)).with_classical_controls("b"),
        cirq.T(cirq.q(0)),
        cirq.T(cirq.q(0)),
        cirq.T(cirq.q(0)),
        cirq.H(cirq.q(0)),
        cirq.measure_each(cirq.q(0)),
    )
def gate_teleportation_on_4_qubits_with_1_magic_state():
    return cirq.Circuit(
        cirq.H.on_each(cirq.q(0), cirq.q(1), cirq.q(2), cirq.q(3), cirq.q(4)),
        cirq.T(cirq.q(4)),
        cirq.measure_single_paulistring(
            cirq.Z(cirq.q(0))
            * cirq.Z(cirq.q(1))
            * cirq.Z(cirq.q(2))
            * cirq.Z(cirq.q(3))
            * cirq.Z(cirq.q(4)),
            key="a",
        ),
        cirq.S(cirq.q(0)).with_classical_controls("a"),
        cirq.S(cirq.q(1)).with_classical_controls("a"),
        cirq.S(cirq.q(2)).with_classical_controls("a"),
        cirq.S(cirq.q(3)).with_classical_controls("a"),
        cirq.measure_single_paulistring(cirq.X(cirq.q(4)), key="b"),
        cirq.Z(cirq.q(0)).with_classical_controls("b"),
        cirq.Z(cirq.q(1)).with_classical_controls("b"),
        cirq.Z(cirq.q(2)).with_classical_controls("b"),
        cirq.Z(cirq.q(3)).with_classical_controls("b"),
        cirq.T.on_each(cirq.q(0), cirq.q(1), cirq.q(2), cirq.q(3)),
        cirq.T.on_each(cirq.q(0), cirq.q(1), cirq.q(2), cirq.q(3)),
        cirq.T.on_each(cirq.q(0), cirq.q(1), cirq.q(2), cirq.q(3)),
        cirq.H.on_each(cirq.q(0), cirq.q(1), cirq.q(2), cirq.q(3)),
        cirq.measure_each(cirq.q(0), cirq.q(1), cirq.q(2), cirq.q(3)),
    )
def gate_teleportation_on_4_qubits_with_4_magic_states():
    return cirq.Circuit(
        cirq.H.on_each(
            cirq.q(0),
            cirq.q(1),
            cirq.q(2),
            cirq.q(3),
            cirq.q(4),
            cirq.q(5),
            cirq.q(6),
            cirq.q(7),
        ),
        cirq.T.on_each(cirq.q(4), cirq.q(5), cirq.q(6), cirq.q(7)),
        cirq.measure_single_paulistring(cirq.Z(cirq.q(0)) * cirq.Z(cirq.q(4)), key="a"),
        cirq.measure_single_paulistring(cirq.Z(cirq.q(1)) * cirq.Z(cirq.q(5)), key="b"),
        cirq.measure_single_paulistring(cirq.Z(cirq.q(2)) * cirq.Z(cirq.q(6)), key="c"),
        cirq.measure_single_paulistring(cirq.Z(cirq.q(3)) * cirq.Z(cirq.q(7)), key="d"),
        cirq.S(cirq.q(0)).with_classical_controls("a"),
        cirq.S(cirq.q(1)).with_classical_controls("b"),
        cirq.S(cirq.q(2)).with_classical_controls("c"),
        cirq.S(cirq.q(3)).with_classical_controls("d"),
        cirq.measure_single_paulistring(cirq.X(cirq.q(4)), key="e"),
        cirq.measure_single_paulistring(cirq.X(cirq.q(5)), key="f"),
        cirq.measure_single_paulistring(cirq.X(cirq.q(6)), key="g"),
        cirq.measure_single_paulistring(cirq.X(cirq.q(7)), key="h"),
        cirq.Z(cirq.q(0)).with_classical_controls("e"),
        cirq.Z(cirq.q(1)).with_classical_controls("f"),
        cirq.Z(cirq.q(2)).with_classical_controls("g"),
        cirq.Z(cirq.q(3)).with_classical_controls("h"),
        cirq.T.on_each(cirq.q(0), cirq.q(1), cirq.q(2), cirq.q(3)),
        cirq.T.on_each(cirq.q(0), cirq.q(1), cirq.q(2), cirq.q(3)),
        cirq.T.on_each(cirq.q(0), cirq.q(1), cirq.q(2), cirq.q(3)),
        cirq.H.on_each(cirq.q(0), cirq.q(1), cirq.q(2), cirq.q(3)),
        cirq.measure_each(cirq.q(0), cirq.q(1), cirq.q(2), cirq.q(3)),
    )
sim = cirq.Simulator()
x_gate_on_1_qubit_circuit = x_gate_on_1_qubit()
result = sim.run(x_gate_on_1_qubit_circuit, repetitions=100)
assert result.histogram(key="q(0)") == collections.Counter({1: 100})
gate_teleportation_on_1_qubit_circuit = gate_teleportation_on_1_qubit()
result = sim.run(gate_teleportation_on_1_qubit_circuit, repetitions=100)
assert result.histogram(key="q(0)") == collections.Counter({1: 100})
gate_teleportation_on_4_qubits_with_1_magic_state_circuit = (
    gate_teleportation_on_4_qubits_with_1_magic_state()
)
result = sim.run(
    gate_teleportation_on_4_qubits_with_1_magic_state_circuit, repetitions=100
)
assert result.histogram(key="q(0)") == collections.Counter({1: 100})
gate_teleportation_on_4_qubits_with_4_magic_states_circuit = (
    gate_teleportation_on_4_qubits_with_4_magic_states()
)
result = sim.run(
    gate_teleportation_on_4_qubits_with_4_magic_states_circuit, repetitions=100
)
assert result.histogram(key="q(0)") == collections.Counter({1: 100})

Craig Gidney · Accepted Answer · 2024-10-23T02:54:39.990

1

The gate that you are applying by teleportation is $(Z^{\otimes 4})^{1/4}$. This is different from $(Z^{1/4})^{\otimes 4} = T^{\otimes 4}$. For example, $(Z^{\otimes 4})^{1/4}$ doesn't phase the $|1100\rangle$ state whereas $(Z^{1/4})^{\otimes 4}$ phases it by 90 degrees.

Here's a quirk circuit with the two gates, so you can see they do different things.

edited Oct 23 '24 at 02:54

answered Oct 23 '24 at 02:38

Craig Gidney

47,099
1
44
119

Does a T gate via teleportation use 1 magic state for $n$ T gates or $n$ magic states for $n$ T gates?

1 Answers1