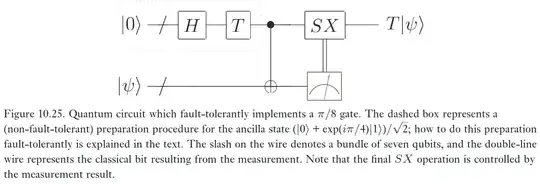
The below figure from page 486 of Nielsen and Chuang, 10th edition shows how a logical gate can be performed on the Steane code. Curiously, to implement the necessary ancilla state, it seems like one needs to apply a $T$ gate transversally, that is, $T$ gates on each of the physical qubits of the ancilla.
How is this possible when the Eastin–Knill theorem says that no code has a transversal universal gateset? I can only think of 2 possible explanations.
- The ancilla, $|0\rangle$, is not encoded in the Steane code but $|\psi\rangle$ is. When the protocol is completed after the classically controlled operation, the logical $T$ gate is applied to a Steane encoded $|\psi\rangle$.
The problem with this explanation is that the textbook explicitly says that the ancilla is encoded into the Steane code at the beginning of the protocol. The book says
The circuit starts with two encoded qubits
- I misunderstand the Eastin–Knill theorem and one can indeed do Transversal $T$ gates on the Steane code, they just can't do it fault tolerantly, hence the need for the gate teleportation protocol. This tracks with an explanation of how to create the ancillary state via a parity measurement of an operator $M$ later in the book on page 491, that moves the transversal $T$ gates to qubits that are not encoded in the Steane code.
To perform the controlled-$M$ operation on the Steane code for the choice of $M$ we apply controlled-$ZSX$ gates transversally for each pair of qubits in the ancilla and the code, followed by seven $T$ gates applied transversally to the ancilla qubits.
So, which one is the answer, and if I didn't list a possible answer, what is it?