For questions regarding $\varepsilon$-$\delta$ definitions of limits, continuity of functions and $\varepsilon-N$ definition of limit of sequences.
The $\varepsilon$-$\delta$ definition of limit of a function is usually first introduced as follows:
Suppose $f(x)$ is a function from $D$ to $\mathbb R$, where $D$ is a subset of $\mathbb R$. If $\forall \varepsilon>0 ~ \exists \delta>0$, such that $0<\vert x-c\vert <\delta\implies \vert f(x)-L\vert<\varepsilon$ for all $x\in D$, then the limit of $f(x)$ at $x=c$ is $L$. Notation: $\lim\limits_{x\to c}f(x)=L$.
Geometrically, this means that if we stay on the graph of $f$, the value of $f(x)$ will be within a distance of $\varepsilon$ from $L$, as long as the distance between $x$ and $c$ is smaller than $\delta$. (See picture.)
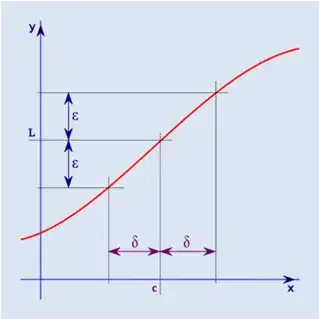
By changing the condition $0<\vert x-c\vert<\delta$ to $0< x-c<\delta$ we get the definition for the right hand limit, notation: $\lim\limits_{x\downarrow c}$, or $\lim\limits_{x\to c^+}$. Similarly, the definition for the left hand limit (notation: $\lim\limits_{x\uparrow c}$ or $\lim\limits_{x\to c^-}$) can be acquired by changing to $0< c-x<\delta$.
In the definition we explicitly stay away from the case $x=c$. This is because we don't require that $f(c)$ be defined.
This definition can very naturally be generalized to the case where $f:(X,d_X)\to (Y,d_Y)$ is a function between metric spaces. Here we have this:
Suppose that $f: D\to Y$, where $D$ is a subset of $X$ and that $c$ is a limit point of $D$. Now we say that $\lim\limits_{x\to c}f(x)=y$ when $\forall \varepsilon>0~\exists \delta>0$, such that $0<d_X(x,c)<\delta\implies d_Y\big(f(x),y\big)<\varepsilon$, for every $x\in D$.
The notion of the $\varepsilon$-$\delta$ definition of a limit or of continuity does not extend to general topological spaces.
The definition of limit of a sequence on a metric space is:
Suppose that $(x_n)_{n\in\Bbb N}$ is a sequence of elements of a metric space $(X,d)$ and that $l\in X$. Then $l$ is the limit of the sequence if $$(\forall\varepsilon>0)(\exists N\in\Bbb N)(\forall n\in\Bbb N):n\geqslant N\implies d(x_n,l)<\varepsilon.$$