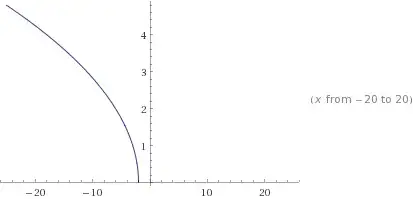
If I try to graph this function, it does not appear to reflect across the y-axis when it comes time to do the reflection. Rather, it is reflected around the point where the function begins on the graph.
Here is what I tried: $$\sqrt{2-x}=\sqrt{-(x-2)}$$ This makes it easier to graph the transformations:
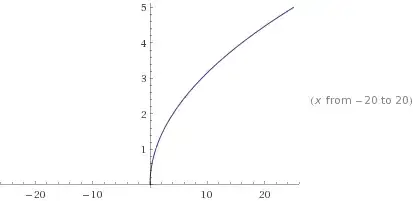
Root function ($f(x)=\sqrt{x}$):
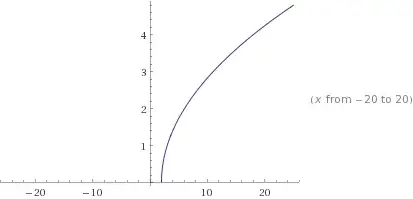
With the right horizontal shift ($f(x)=\sqrt{x-2}$):
With a horizontal reflection ($f(x)=\sqrt{-(x-2)}$):
This is the part I'm confused about. Why doesn't it reflect across the y-axis?
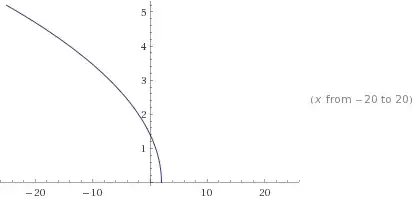
I would expect the final graph to look like this: