1

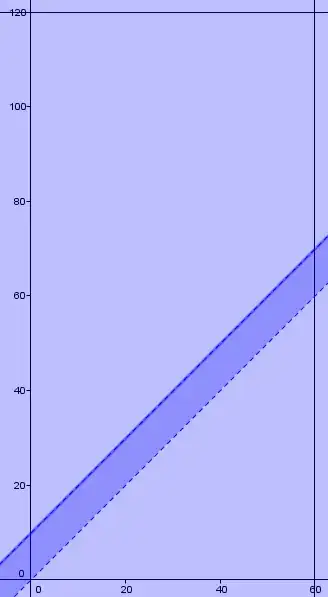
A and B are going to the math palace. A arrives between 12:00 and 13:00 o'clock and stays for 10 minutes, whereas B arrives between 12:00 and 14:00 o'clock and leaves immediately. The time point in which they arrive is uniformly distributed on the stated intervals. What is the probability that A and B meet each other?

My try:

P($X_{B}\in [X_{A}-10m;X_{A}+10m]) = F_{X_{B}}(X_{A}+10m)-F_{X_{B}}(X_{A}-10m)$

$= \frac{X_{A}+10m-12h}{14h-12h} - \frac{X_{A}-10m-12h}{14h-12h} = \frac{1}{6}$

Which is wrong. The correct solution would be $\frac{1}{12}$

Bolz
  • 453

2 Answers2

3

I've got an alternative solution, done quite differently: Let $x$ be the time at which $A$ arrives and $y$ be the time at which $B$ arrives. Also, instead of considering the time, we consider the number of minutes from 12:00, i.e. $0<x<60$ and $0<y<120$ which is our sample space. In addition to that, we know that $A$ must arrive before $B$, so $y>x$ because if $B$ arrives first, he/she will leave immediately. Lastly, we know that after $A$ arrives at $x$, $B$ must arrive within 10 minutes, which means $y-x \leq 10$. Now we have two inequalities $$y\leq x + 10 \\ y>x$$ where $0<x<60$ and $0<y<120$. Plotting these yields the following graph: Graph

The ratio of the dark blue area to the whole rectangle is $1/12$.

Sheheryar Zaidi
  • 2,754
1

P($X_{B}\in [X_{A};X_{A}+10m]) = F_{X_{B}}(X_{A}+10m)-F_{X_{B}}(X_{A})$

$= \frac{X_{A}+10m-12h}{14h-12h} - \frac{X_{A}-12h}{14h-12h} = \frac{1}{12}$

Karel Macek
  • 767