Which power means are constructible?

Question

The three classic Pythagorean means $A$, $G$, $H$ (arithmetic, geometric, and harmonic mean respectively) of positive real $a$ and $b$ have a cute geometric construction, as does the quadratic mean $Q$:

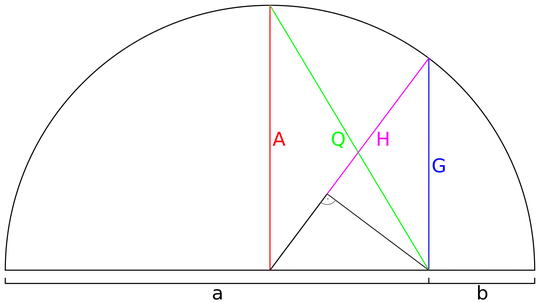
pythagorean means

From this picture the ordering of these power means is directly visible.

What I'm curious about is whether there are other examples of such constructible power means (i.e. $M_q=\left(\frac{a^q+b^q}{2}\right)^{1/q}$). Obviously not all means will work; for instance, it will not be constructible if it can map two constructible numbers to an unconstructible number. The question is which ones are possible, and how they would be explicitly constructed.

$n$-th roots are not constructible unless $n$ is a power of $2$. All integer powers are constructible so the constructible ones are $M_{2^k}$ — Darth Geek, Aug 15 '14 at 14:44
@DarthGeek: Makes sense. Do you know how one would construct $M_{2^k}$ in the spirit of the above diagram? I imagine it gets tedious quickly, but a standard algorithm for such seems plausible. — Semiclassical, Aug 15 '14 at 14:48
@DarthGeek I think you want $M_{\pm 2^{k}}$, because $M_{-1}=H$ above... — Thomas Andrews, Aug 15 '14 at 14:48
@ThomasAndrews That's right! I don't know if those means can be easily found as in the diagram, but they can be constructed using the construction of a the sum of two segmenta, the product of two segments and the square root of a segment the old fashion way... — Darth Geek, Aug 15 '14 at 14:52
@DarthGeek Is that fact about constructability of $n$-th roots applicable to real $n$ or just to integer $n$? For example, the statement seems to ignore values like $n=1/3$. If it only resolves the question for integral $n$, then more is needed to answer the original question for all real $q$. — Matt, Aug 19 '14 at 02:04
@Matt Any integer power is constructible but only $2^k$-th roots are constructible. Therefore, you can only construct means of the form $M_{\pm 2^k}$ — Darth Geek, Aug 19 '14 at 08:05
@DarthGeek: Yes, that's what you said before, but the question is how complete that answer is. The result that "only $2^k$-th roots are constructable" is, as I understand it, only applicable to questions about $n$-th roots, with $n \in \mathbb N^+$. (As circumstantial evidence, we do not say "only $2^k$-th roots and $1/k$-th roots are constructable.") And there are many other cases. The power means are defined for all $q\in[-\infty,\infty]$. They are certainly constructable for $q=-\infty$ and $q=\infty$, for example. — Matt, Aug 19 '14 at 09:13
@Matt yes, and by "only" I meant that the power means $M_q$ for $q \neq \pm 2^k$ is not constructible. We could consider $M_{-\infty}$ and $M_\infty$ as $\lim_{k\to\infty} M_{\pm2^k}$ just as $M_{-\infty}$ and $M_\infty$ are defined as $\lim_{q\to\infty} M_{\pm q}$. — Darth Geek, Aug 19 '14 at 09:34
@DarthGeek: Yes, it is very clear (even from the beginning) what you meant. What is not clear is your reasoning for thinking this is a complete answer. You have extended your answer twice now (and it still doesn't include the geometric mean) -- using a clear line of reasoning would help to avoid these problems, as well as help convince someone who doesn't just believe whatever they hear. — Matt, Aug 19 '14 at 09:58
@DarthGeek: Can you convert that into a (possibly partial) answer? — Semiclassical, Aug 19 '14 at 12:05
For many of the products, quotients and square roots, having a reference unit is required. If only $a$ and $b$ are given, I don't know how to create any more power means than the ones showed by your picture. — Darth Geek, Aug 19 '14 at 16:51
@DarthGeek: A reference unit should not be required, since all the means are scale-invariant: $M_q(c\cdot a,c\cdot b)=c\cdot M_q(a,b)$. Or, in other words, you can use whatever you want as the reference unit; the final answer will not be affected by your choice. — Matt, Aug 20 '14 at 18:49
@Semiclassical, what's the source of this nice diagram, yours? The classical civilizations knew 10+ distinct means, as discussed here: http://www.tandfonline.com/doi/abs/10.1198/tast.2009.0006#.U_VjeIBdVRY. Are all described by line segments in a semicircle? — alancalvitti, Aug 21 '14 at 03:10
@alancalvitti: Alas, no---it's from Wikipedia. (I should edit the question to link to that.) And I'm not versed in the remainder of the Pythagorean means, so I can't weigh in there; given the Greek use of geometry instead of algebra, though, it seems quite likely. — Semiclassical, Aug 21 '14 at 03:13
@DarthGeek: FYI, the grace period on the bounty has started. So if you're still interested in giving an answer, now is the time to do it... — Semiclassical, Aug 25 '14 at 21:34

score 1 · Answer 1 · answered Jan 08 '16 at 16:11

1

For an algebraic number over $\mathbb Q$, in order to be constructable it's minimal polynomial should be of a degree $2^n$ , thus $M_{2^n}$

answered Jan 08 '16 at 16:11

user26977

1,118

score 1 · Answer 2 · edited Apr 13 '17 at 12:20

This is a construction for $M_4$:

$AC=a$ and $AK=b$.

Using a dummy unit length $(AB)$ you construct $GH=a^4$ and $NO=b^4$ (example for $a^2$ construction).

Let $BQ=a^4+b^4$, $R$ is the middle point for $BQ$ so $BR=(a^4+b^4)/2$.

Using the same dummy unit we construct the square root $BT$ of $BR$ and the square root $BW$ of $BU=BT$.

We now have your desired mean. The dummy unit is uninfluent, if you change the lenght of $AB$ the length of $BW$ does not change.

Which power means are constructible?

2 Answers2