0

If we have a linear length of "$A$" in page, How can I draw (construct) a "$A^2$" with non-graded ruler and compass?
Is it possible to help me? Sorry for bad English.
Thanks.

Amin Borjian
  • 175
  • Your question does not make sense. If $A = 1\mathrm{cm}$, then $A^2 = 1 \mathrm{cm}^2$ is an area and not a length. – gerw Dec 18 '15 at 12:28
  • @gerw In mathematics we usually don't need to asign units to our lengths or areas. However as the answers below point out we still need a lenght of 1 in order to make sense of what a length of $A^2$ means. And then the question makes perfect sense. If we have a length of A cm then we can construct a length of $A^2$ cm. – Jorik Dec 18 '15 at 12:37

2 Answers2

4

Without a unit length, you cannot do this. If you have a unit length, you can do it as follows:

Draw a line, and mark three points $p_0$, $p_1$ and $p_A$ on it, such that $|p_0-p_1| = 1$ and $|p_A - p_0| = A$. Through $p_0$, draw a second line $\ell_2$, different from the first, mark a point $q_1$ on it such that $|q_1 - p_0| = A$. Draw a line through $p_A$, parallel to $p_1q_1$. This line intersects $\ell_2$ in a point $q_A$ with $|q_A - p_0| = A^2$ due to the intercept theorem.

martini
  • 86,011
4

For a length of $A^2$ to even make sense you need to also have a length of 1. So I'm going to assume that we already have the line segment from $(0,0)$ to $(1,0)$.

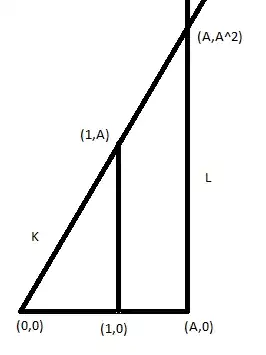
Then first construct the point $(A,0)$ by extending the line segment of lenght one to length $A$. Then construct a line through $(1,0)$ that is at a right angle to the line between $(0,0)$ and $(1,0)$. Mark a distance of $A$ along this line as well so that we get the point $(1,A)$. Next construct the line L through $(A,0)$ that is at a right angle to the line between $(0,0)$ and $(A,0)$. Now draw the line $K$ through $(0,0)$ and $(1,A)$. The intersection between $L$ and $K$ will be at $(A,A^2)$. And so we have a distance of $A^2$.

Here is a picture of the construction:

Image of construction

EDIT: The reason we need the segment of length 1 is the following. Assume we could construct a segment of length $A^2$ from only a segment of length $A$. Now use this construction starting with a length of $2A$. This construction should look exactly the same except blown up by a factor of $2$. This would lead to the result that $(2A)^2=2(A^2)$ which is nonsense.

Jorik
  • 1,421
  • Thanks for answer. It's true. I accept it. I will ask my teacher for length of 1. I asked him for help and he said you can do it in circle. However thanks. – Amin Borjian Dec 18 '15 at 12:46
  • @AminBorjian I'll add the reason why we need it to my answer. – Jorik Dec 18 '15 at 12:49