How one can check the function whether it is convex or not. I know one method by using Hessian Matrix but I think it did not fit for the following example.
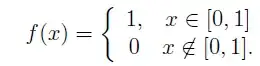
I think Hessian matrix method cannot be used for this case.
How one can check the function whether it is convex or not. I know one method by using Hessian Matrix but I think it did not fit for the following example.
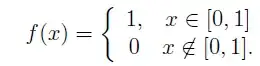
I think Hessian matrix method cannot be used for this case.
Hint Looking up the definition on Wikipedia, we have that $f$ is convex iff for any $x_1, x_2 \in \Bbb R$ and $t \in [0,1]$:
$$f(tx_1 + (1-t)x_2) \leq tf(x_1) + (1-t)f(x_2)$$
Now, let (for example) $x_1 = -1/2$ and $x_2 = 1/2$. Can you find a $t \in [0,1]$ so that the above does not hold?
I believe you have to check if you have two elements in the image if the function, then any point on the line drawn between them must be above the image.
Using your example for $f(x)$, suppose $x_{1}, x_{2} \in \mathbb{R}$ and $t \in [0, 1]$. We need to show $f(tx_{1} + (1-t)x_{2}) \leq tf(x_{1}) + (1 - t)f(x_{2})$.
Now, to check that the inequality holds, we have to check all possible cases.
Case 1: Suppose both $x_{1}$ and $x_{2}$ are in $[0,1]$. Then so is any point on the line between them, which means $f(tx_{1} + (1-t)x_{2}) = 1$ and $1 \leq t(1) + (1 - t)(1)$.
Case 2: Suppose $x_{2} \in [0,1]$ but $x_{1} \not \in [0,1]$. Then for some values of $t$, the point on the line is in $[0,1]$ and for others it is not. Then if $t$ is such that the point $tx_{1} + (1-t)x_{2} \in[0,1]$, we have $$f(tx_{1} + (1-t)x_{2}) = 1 \not \leq t*f(x_{1}) + (1-t)*f(x_{2}) = t*1 + (1-t)*0 = t.$$ Why is $1 \not \leq t$ here? Because we needed $t$ so that the point on the line is in $[0,1]$. If $t = 1$, then the point on the line is $1*x_{1} + 0*x_{2} = x_{1} \not \in [0,1]$ by assumption, so $t < 1$.
Thus, since $t < 1$ we have $f(tx_{1} + (1-t)x_{2}) = 1 \not \leq t*1 + (1-t)*0 = t$ for some $t$, and so we found a point on the line that is not above the function, which means $f$ is not convex.
Every convex function is continuous.