2

Let $\mathcal N$ be an exact category and $C\mathcal N$ be the category of chain complexes with its usual exact structure. We have here the usual notion of "mapping cylinder" of a chain map. If $f:N\to M$ is a chain map, denote by $T(f)$ its mapping cylinder. Denote by $j_1:N\to T(f)$ and $j_2:M\to T(f)$ the inclusion on the first and third factors respectively. These are admissible monomorphisms.

Suppose we have a commutative diagram in $C\mathcal N$:

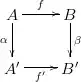
enter image description here

where $\alpha$ and $\beta$ are admissible monomorphisms.

Let $t:T(f)\to T(f')$ be the induced map; that is, $t=\left(\begin{smallmatrix} \alpha & 0 & 0 \\ 0 & \alpha[-1] & 0 \\ 0 & 0 & \beta \end{smallmatrix}\right)$.

I want to prove that the induced arrow $s$ in the pushout diagram below is an admissible monomorphism:

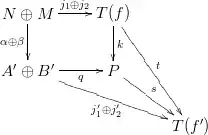
enter image description here

Notice that every arrow there but $s$ is an admissible monomorphism.

So I was able to show that $s$ has a cokernel (it's the cokernel $e$ of the map $T(f)\oplus (A'\oplus B') \to T(f')$ given by the matrix $(t \hspace{.6cm} j_1'\oplus j_2')$).

But I'm stuck at showing that $s$ is also the kernel of $e$. I've tried several different things for a couple of days now but I'm just absolutely stuck...

Bruno Stonek
  • 12,973

1 Answers1

1

It's probably easiest to compute $P$ and the map $s$ explicitly. It turns out that $P$ has components $P_n = A_{n}' \oplus A_{n-1} \oplus B_{n}'$ and that $s_n = 1_{A_{n}'} \oplus \alpha_{n-1} \oplus 1_{B_{n}'}$, which is obviously an admissible monomorphism since it is the direct sum of admissible monomorphisms.

Some details, using Weibel's sign conventions on p.20:$\require{AMScd}$

The complex $T(f)$ has components $A_{n} \oplus A_{n-1} \oplus B_n$ and differential $\begin{bmatrix} d^{A}_{n} & 1_{A_{n-1}} & 0 \\ 0 & -d^{A}_{n-1} & 0 \\ 0 & -f_{n-1} & d^{B}_{n} \end{bmatrix}$, similarly for $T(f')$.

In each degree $n$ there is the push-out diagram $$\begin{CD} A_n \oplus B_n @>{\begin{bmatrix} 1 & 0 \\ 0 & 0 \\ 0 & 1\end{bmatrix}}>> A_n \oplus A_{n-1}\oplus B_n @>{\begin{bmatrix} 0 & 1 & 0 \end{bmatrix}}>> A_{n-1} \\ @VV{\begin{bmatrix} \alpha_n & 0 \\ 0 & \beta_n\end{bmatrix}}V @VV{\begin{bmatrix} \alpha_n & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & \beta_n \end{bmatrix}}=k_nV @| \\ {A_{n}' \oplus B_{n}'} @>>{\begin{bmatrix} 1 & 0 \\ 0 & 0 \\ 0 & 1\end{bmatrix}}=q_n> {A_{n}' \oplus A_{n-1} \oplus B_{n}'} @>>{\begin{bmatrix} 0 & 1 & 0 \end{bmatrix}}> A_{n-1} \end{CD}$$ from which you can see that $P_n = A_{n}' \oplus A_{n-1} \oplus B_{n}'$. Contemplating the push-out above, you can convince yourself that the differential of $P$ must be given by the matrix $$ \begin{bmatrix} d_{n}^{A'} & \alpha_{n-1} & 0 \\ 0 & - d_{n-1}^A & 0 \\ 0 & -\beta_{n-1} f_{n-1} & d_{n}^{B'} \end{bmatrix} $$ and that the induced map $s_n\colon P_n \to T(f')$ is given by $s_n = 1_{A_{n}'} \oplus \alpha_{n-1} \oplus 1_{B_{n}'}$, as desired.

Note also that this shows that the cokernel of $s$ is equal to the cokernel of $\alpha[-1]$.

  • Great! In fact, not too many days ago I managed to solve the problem with help from my supervisor, and I was planning to post it here very soon. I got the same thing as you though I had to use elements to be convinced that the $P$ you define is effectively the pushout, etc. Thanks a lot for your effort on an already old and quite ignored question. – Bruno Stonek Jun 17 '14 at 17:56
  • For the prospective reader, I might add that the easy observation that the forgetful functor from $C\mathcal N$ to the category of graded objects over $\mathcal N$ reflects exactness is implicitly being used. – Bruno Stonek Jun 20 '14 at 17:13