46

Let's fix some terminology first. A category $\mathcal{C}$ is preabelian if:

1) $Hom_{\mathcal{C}}(A,B)$ is an abelian group for every $A,B$ such that composition is biadditive,

2) $\mathcal{C}$ has a zero object,

3) $\mathcal{C}$ has binary products,

4) $\mathcal{C}$ has kernels and cokernels.

A category $\mathcal{C}$ is abelian if it is preabelian and satisfies:

5) every monomorphism is a kernel and every epimorphism is a cokernel.

Define the coimage of a map to be the cokernel of its kernel, and the image to be the kernel of its cokernel. We have the following commutative diagram:

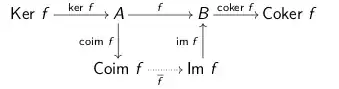
enter image description here

where $\overline{f}$ is the only existing map (because of universality of kernel and cokernel).

I'm having trouble proving the following:

A preabelian category $\mathcal{C}$ is abelian iff $\overline{f}$ is an isomorphism.

The converse is easily shown, I'm having trouble proving $\Rightarrow$...

Bruno Stonek
  • 12,973
  • Can you prove that $\overline{f}$ is both a monomorphism and an epimorphism if $\mathcal{C}$ is abelian? – t.b. Jun 12 '11 at 21:01
  • @Theo: I'm trying. But is it true in an abelian category that mono-epi is iso? – Bruno Stonek Jun 12 '11 at 21:11
  • Yes. That's exactly my point. – t.b. Jun 12 '11 at 21:16
  • @Theo: I'm having difficulties proving that $\overline{f}$ is mono, anyway. I'm trying to prove that $Ker(\overline{f})=0$ by using the universal property of ker, but I'm not seeing how every other map $X\to Coim(f)$ factors through zero... – Bruno Stonek Jun 12 '11 at 21:25
  • @Theo: would you consider posting an answer? Thank you very much. – Bruno Stonek Jun 12 '11 at 22:06
  • 3
    Sorry for not following up earlier. It's not trivial at all. You can extract a proof from chapter 2 of Freyd's book where it basically occupies the entire section. It's getting late here and there's the danger that I get myself hopelessly confused when trying to find some short cuts. – t.b. Jun 12 '11 at 22:32
  • To ensure that you don't get stuck right at the start, this answer of mine should help establishing Freyd's Axiom A1* from yours. The theorem you're after is the unique factorization theorem 2.19 on page 70 of the pdf I linked to. – t.b. Jun 12 '11 at 22:42
  • @Theo: Thank you, I'm aware that product and coproduct coincide with biproduct. I shall take a look at Freyd; I already had, but I didn't recognize it under that name and (to my taste) awkward wording. – Bruno Stonek Jun 12 '11 at 22:43
  • 1
    That the map $\operatorname{Coim}f \to B$ is monic is Freyd's Theorem 2.18$^\ast$ on page 70 of the pdf (page 44 of the book). This implies that $\bar{f}$ is monic. Dually, $\bar{f}$ is epic (use Thm 2.18 on page 69 (43)). Then Theorem 2.12 on page 66 (37) shows that $\bar{f}$ is an isomorphism because it is monic and epic. – t.b. Jun 12 '11 at 22:48
  • @Theo: I see. Combining Freyd's theorems 2.12, 2.18 and 2.18* with Mac Lane's CWM proposition 1 in page 195 (the analogue of Freyd's "unique factorization"), I believe I can write a tidy proof. I shan't do so today, though. Thank you for your assistance. – Bruno Stonek Jun 12 '11 at 22:55
  • You're welcome, glad I could help. Ping me in case you're getting stuck. By the way: unique factorization because in an abelian category every map has a unique decomposition as an epic followed by a monic (unique up to iso, of course). In other words, it factors uniquely over its coimage = image. – t.b. Jun 12 '11 at 23:07
  • @Theo: I still can't do it. The answer seems to be hidden in Freyd's book, which I find quite unreadable. I put it aside and tried to prove that $\overline{f}$ is mono-epi, so this would prove that it is iso. I couldn't do it, and in fact, I'm also unable to prove that in an abelian category mono-epi implies iso. What a failure!

    I wonder whether it is true, in fact, that mono implies section and epi implies retraction?

     – Bruno Stonek Jun 14 '11 at 00:57
  • 4
    a) Consider $0 \to \mathbb{Z}/2 \to \mathbb{Z}/4 \xrightarrow{\cdot 2} \mathbb{Z}/2 \to 0$ for a counterexample to the last question (abelian groups are an abelian category, of course). b) If $g: A \to B$ is mono-epi then its kernel is zero $0 \to A$ and epis are cokernels of their kernels in an abelian category. Now the composition $0 \to A \xrightarrow{1_A} A$ is zero, so $1_A = hg$ for some $h: B \to A$. On the other hand $ghg = 1_Bg$, so $gh = 1_B$ and hence $h$ is inverse to $g$. – t.b. Jun 14 '11 at 01:07
  • Don't be too hard on yourself, I told you it wasn't trivial! I'll post something soon (but I need to sleep first). – t.b. Jun 14 '11 at 01:10
  • @Theo: again, thank you very much. I'm absorbing your previous comment right now. I don't quite get your "on the other hand", it seems you're using that $g$ is a retraction, but that isn't necessarily so. In any case, dually you get a right inverse, and existence of right and left inverse implies iso. Also, you're using that if f is epi then it's the cokernel of its kernel: I didn't know that (I think that's what Freyd proves on 2.11... "Ker and Cok are inverse functions", come on...) – Bruno Stonek Jun 14 '11 at 01:46
  • 2
    Yes, I know you don't like Freyd's way of writing :), yes that's what I'm using (that's not hard). No In the "on the other hand..." I'm just using that $g$ is epi: If $kg = lg$ then $k = l$ applied to $(gh)g = g(hg) = g1_A = g = 1_Bg$ thus $gh = 1_B$. – t.b. Jun 14 '11 at 01:54

1 Answers1

53

Here is an argument for $\Rightarrow$. There is not much more to it than chasing diagrams (as it should be). Also, I didn't really bother to check which (parts of the) axioms are actually needed:

  1. In presence of 1),2),3) we have that $\mathcal{C}$ has biproducts as well: every binary coproduct is also a binary product. (This is not used below but I added it for the sake of completeness)

  2. Assuming 1)-5), an epi $e:B \to C$ is the cokernel of its kernel. cokernel of kernel diagram
    Indeed, let $f$ be a morphism such that $e = \operatorname{coker}\,{f}$ and let $k = \operatorname{ker}{e}$. Since $ef = 0$, we see that $f = kf'$. If $y$ is such that $yk =0$ then $ykf' = yf = 0$ and hence $y = y'e$, and thus $e$ is a cokernel of $k$.

    Dually, a mono is the kernel of its cokernel.

  3. Assuming 1)-5) a morphism which is both an epimorphism and a monomorphism is an isomorphism.

    I leave that as an easy exercise (I gave the argument in the comments above).

  4. Let $f: A \to B$. The morphism $i: \operatorname{Coim}{f} \to B$ is monic.i monic
    To this end, let $x: X \to \operatorname{Coim}{f}$ be such that $ix = 0$. Let $q = \operatorname{coker}{x}$ and let $j: \operatorname{Coker}{x} \to B$ be the unique map such that $i = jq$. Since $qp$ is epi we have a morphism $h: H \to A$ such that $qp = \operatorname{coker}{{h}}$. Now $fh = iph = jqph = 0$ so $h = kh'$. This gives that $ph = pkh' = 0$, factorization of p
    so $p$ factors as $p = p'(qp) = (p'q)p$. But $p$ is epi, so $p'q = 1_{\operatorname{Coim}{f}}$. This implies that $q$ is a monomorphism and finally $qx = 0$ implies that $x = 0$. We have shown that $ix = 0$ implies $x = 0$ and thus $i$ is a monomorphism.

    Dually $j: A \to \operatorname{Im}f$ is an epimorphism.

  5. Consider the factorization of $f$: Analysis of a morphism By step 4 we have that $A \to \operatorname{Im}{f}$ and $\operatorname{Coim}{f} \to B$ are epi and mono, respectively. Therefore $\bar{f}$ is both epi and mono and we're done by step 3.

Community
  • 1
t.b.
  • 80,986
  • @Theo: Thanks! I'm digesting your answer. I don't understand this part, though: "Since e is epi, this factorization is unique and hence e is a cokernel of k." – Bruno Stonek Jun 14 '11 at 14:12
  • @Bruno: If $y'e = y = y''e$ then $y' = y''$ since $e$ is epi. Thus every $y$ with $yk=0$ factors uniquely as $y = y'e$ over $e$, and this, together with $ek = 0$ is the definition of $e$ being a cokernel of $k$. – t.b. Jun 14 '11 at 14:23
  • @Theo: If I understand correctly, since $e=coker(f)$ and $y$ is another map such that $yf=0$, then there exists a unique $y'$, by definition of cokernel, no? I don't see how it is needed to use again that $e$ is epi. – Bruno Stonek Jun 14 '11 at 14:30
  • @Bruno: Yes, you're right. It's not necessary. Be that as it may, there is only one factorization $y = y'e$. – t.b. Jun 14 '11 at 14:39
  • @Bruno: Is there something missing in this argument? Note that I used the following implicitly a few times: If $ji$ is mono then $i$ is mono because $ix = 0$ implies $jix = 0$ and hence $x = 0$ because $ji$ is mono. Please ask if you need further clarifications. – t.b. Jun 15 '11 at 13:19
  • 1
    @Theo: Sorry, I hadn't had time to finish checking the argument. I did now, it's perfect. Thank you once again, you've been of huge help! – Bruno Stonek Jun 15 '11 at 15:43
  • 3
    @Bruno: Thank you, that's nice to hear! By the way: If you want to test your understanding of this argument try to prove the following: Let $k: A' \to A$ be a monomorphism and let $f': A' \to B'$ be an arbitrary morphism. Consider the push-out diagram $$\begin{array}{ccc} A' & \xrightarrow{k\phantom{l}} & A \ \downarrow{\scriptstyle{f'}} & \tiny{\text{PO}} & \downarrow{\scriptstyle{f}} \ B' & \xrightarrow{\phantom{k}l} & B. \end{array}$$ Then $l$ is a monomorphism. "The push-out of a mono along an arbitrary morphism is a mono." Dually the pull-back of an epi is an epi. – t.b. Jun 15 '11 at 22:23
  • @Bruno: Note that the push-out $B$ can be constructed by taking the cokernel $B$ of $\begin{bmatrix} k \ -f' \end{bmatrix}: A' \to A \oplus B'$ and writing it as $\operatorname{coker}{\begin{bmatrix} k \ -f' \end{bmatrix}} = [,f;;; l,]: A \oplus B' \to B$. As a hint for the previous comment, I'd break $f'$ into epi and mono first and deal with these two cases separately. Then the general case follows from the observation that two push-out diagrams glued along a common arrow again is a push-out diagram. Warning: It's not an easy exercise. – t.b. Jun 15 '11 at 22:28
  • 3
    @Bruno: Third and last comment (self-advertisement): As a motivation for this exercise, look at exact categories on Wikipedia. I've written a survey on these some years ago - one point is that exact categories are very convenient for proving the standard diagram lemmas and you can do practically all the homological algebra in them. If you can't access it, there's a preliminary version of it on the ArXiV. – t.b. Jun 15 '11 at 22:34
  • 4
    Part 3 is proven in your comments above, and it is perfectly fine. Here is a proof which does not use that the coimage of an epimorphism is the same morphism. Let $f:A\to B$ be mono-epi. Then $f=ker g$ for some $g:B\to X$. Then $gf=g(kerg)=0=0f$: since $f$ is epi this implies $g=0$. But then $f=ker g=ker 0=Id_B$ hence $f$ is an isomorphism. @Theo – Bruno Stonek Jul 06 '11 at 00:49
  • @Bruno: That's right and probably a bit easier than what I wrote, thanks! But what I see as the really non-trivial ingredient remains the same: axiom 5) of your list in the question. – t.b. Jul 06 '11 at 13:45
  • @t.b. I've been trying to work out this theorem and related material for myself for the last couple of days. I got for myself the canonical morphism from coproducts to products in categories with zero morphisms, and that this is iso in preadditive categories, and the canonical morphism from coimage to image. I didn't make much progress in showing that this morphism was iso in Abelian categories, and after being stuck for a while, I searched online and found this thread [...] – ziggurism May 30 '12 at 03:44
  • 1
    @t.b. What I really liked about your answer was your outline. I was able to read the steps necessary, and show them myself, instead of just reading the proof. That was very valuable! Actually, I was able to do your steps 1-3, and 5 myself, but have not yet cracked step 4, which I guess is the big one. But I'll keep working on it for a while, and if I don't get it myself eventually, I'll read it here. This was a really great answer. Thanks! – ziggurism May 30 '12 at 03:46
  • 1
    @ziggurism: thanks, that's very nice to hear! Yes, 4. is the tricky part of the argument. I'm sure you can figure it out, but I have to admit that it took me a moment, too. – t.b. May 30 '12 at 05:45
  • 1
    @t.b.: Almost three years later, I got to the point where I need to get into exact categories (as I seem to be getting into algebraic K-theory...) and your article seems to be the current standard reference. And it is a joy to read, your exposition is wonderful! It's sad that you don't hang around here anymore... Perhaps you will see this comment, and perhaps by the time you see it this question which shouts your name will have been answered already. – Bruno Stonek May 16 '14 at 23:46
  • 1
    Where is step 2 used? Step 5 only seems to use steps 3 and 4, and neither 3 nor 4 do seem to use step 2 on their proofs. – Elías Guisado Villalgordo Feb 28 '22 at 18:26