A straight line in 2-D $x+y=3$ and a circle in 2-D $x^2+y^2=4$ do not have a point of intersection in the plane containing the two. But on solving these equations analytically, on gets 2 complex solutions $x=1.5+0.5i,y=1.5-0.5i$ and $x=1.5-0.5i,y=1.5+0.5i$. I was trying to interpret this geometrically and since it did not make sense on a plane, I moved to 3-D. I defined a complex space with the $z$-axis being the "imaginary" axis and retained $x$ & $y$ as such. But though I am able to plot these 4 points and visualize them, I am not able to relate them to the plane. Any help in understanding the solution geometrically either through this approach or any other approach would be appreciated…
1 Answers
3D is only oflimited use, since both your original dimensions are complex, so you'd have to move to 4D do accurately embed this. And I for one have some trouble imagining 4D, so I'm not sure there is anything to be gained from this endeavor.
You can simplify the situation a bit by considering a line like $x=3$, i.e. one which is parallel to one of the axes of your original coordinate system. Then you can concentrate on the part of $\mathbb C^2$ where $x\in\mathbb R$, and interpret that in three dimensions. So we are essentially speaking about points of the form $(x, y + iz)$.
So what is the line in this setup? It's a plane, namely the plane $x=3$. And what is the circle? Let's compute that.
$$x^2+(y+iz)^2 = x^2 + y^2 - z^2 + 2yzi = 4 \\ yz=0 \quad\text{and}\quad x^2+y^2-z^2 = 4$$
The first of these conditions is the union of the $y=0$ and the $z=0$ planes. For $z=0$, the second equation is our well-known circle $x^2+y^2=4$ in the original $xy$ plane. For $y=0$ this is the hyperbola $x^2+z^2=4$. So you can imagine the 3d image of your circle as the union of a circle in one plane and a hyperbola in a different plane, where both of these planes are orthogonal to one another.
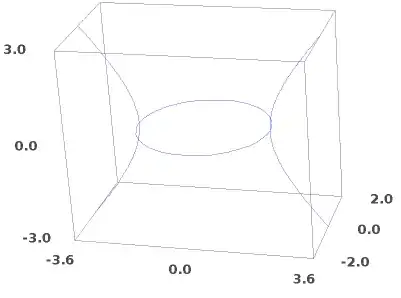
As you move the line from e.g. $x=1$ to $x=3$ in the 2D image, you are moving that plane in 3d from the situation where it intersects the circle to the situation where it intersects the hyperbola. In between there is the situation where there is only a single point of intersection, where your line is a tangent to the circle.
Keep in mind that this whole image depends a lot on the orientation of the line. You can try to imagine that by rotating the orientation of your line, you'd have to rotate the plane of the hyperbola as well, because hyperbola and circle still have to touch in the tangency situation. So you get a glimpse at the 4d structure after all: this rotation of the line would be your fourth dimension.
- 44,006
-
First up, why do I need to take to replace y with y+iz in the original equation? I am only interested in plotting the real co-ordinates of the graph & how this real figure is capable of generating a complex solution. Secondly, you haven't explained what the solution means geometrically. For instance, in the case which you showed, substituting x=3 yields an absurd result y=+sqrt(5)i & y=-sqrt(5)i. The second equation of the hyperbola gives the correct result, but I again do not understand what it means geometrically & why such a roundabout approach is needed in the first place. – K.R. Manish Apr 25 '14 at 16:50
-
@K.R.Manish: Since I am using the $z$ direction or $\mathbb R^3$ to plot the imaginary component of the original $y$ coordinate, $(x,y,z)$ in 3d corresponds to $(x,y+iz)$ in the plane. I feel we might have different views with regard to “geometric meaning”, but I don't know how to put even that difference in words. E.g. I wouldn't call $(3,\pm\sqrt5i)$ an absurd result, and in my image that's simply where the plane intersects the hyperbola. I guess the main point of my approach is to give you an idea of how the circle “extends” into $\mathbb C^2$. Is that “meaningful” to you? – MvG Apr 25 '14 at 17:34
-
yes, 3 + sqrt(5)i is meaningful to me too.... but the problem is since you have already defined y+iz in 3-d, y & z are real... but the imaginary solution contradicts this initial assumption..... On the other hand, z=sqrt(5) is meaningful as it denotes points where the plane cuts the hyperbola.... but I want to know how the hyperbola came about in the first place... Yes, I want to know how it "extends" into 3-d & how the line "extends" into a plane, since these were not there originally... Could you elaborate on this aspect? – K.R. Manish Apr 26 '14 at 16:15
-
@K.R.Manish: It's the same construction which turns the real line $\mathbb R$ into $\mathbb C$ which you can then vidualize as a plane isomorphic to $\mathbb R^2$, simply by translating $a+bi$ to $(a,b)$. Only this time we have the $x$ coordinates to carry along, which are unaffected by this conversion on $y$ and $z$. – MvG Apr 26 '14 at 16:26