-1

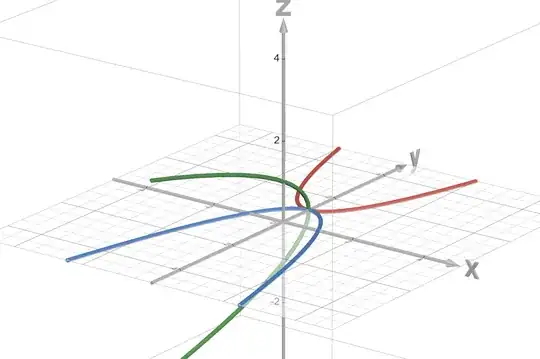
My question is similar to this one but hopefully simpler. See the attached image below I created on Desmos. 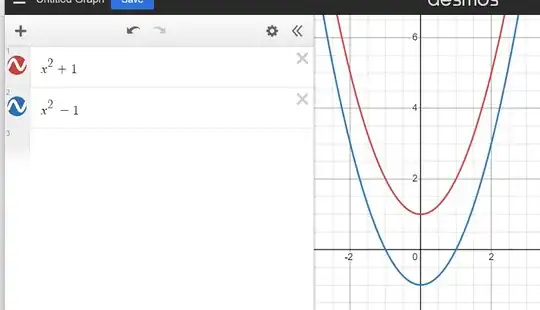Plot of two Parabolas Now, the zeroes for the blue parabola are $x = -1$ and $x = 1$. The zeroes for the red parabola are $+i$ and $-i$. The geometric interpretation for the former is easily understood as the intersection of the parabola with the x axis. But I am struggling to find a geometric interpretation for the latter. Based on Angae MT's comments, I took another stab at drawing this, where the z axis is imaginary and the BLUE parabola represents the reflection that Angae is speaking of and the GREEN represents the same parabola but rotated 90 degrees. The only difference is that it is plotted in 3D with the 3rd axis being imaginary. I tried to upvote MT Angae's answer but I don't have sufficient reputation.

3D of Angae's Answer

2

Haris
  • 3,587
Rasputin
  • 3
  • If you are working with complex numbers, you need to plot accordingly. Since complex numbers have real and imaginary part, the plot will be a surface, not a curve. – Vasili Mar 28 '24 at 20:25
  • I'd say you need 4-dimensional graph paper to plot complex functions of a complex variable. – Gerry Myerson Mar 28 '24 at 22:31
  • @GerryMyerson R2 has an x axis and y axis. The complex plane has an x axis and an imaginary axis. So I would have thought (but am probably wrong) that since the two planes share a single x axis (which is real in both planes) that you could show both on the same 3D graph like I did in my second picture above where the z-axis is imaginary. I think you may be suggesting that the x axis in the complex plane is not the same as the x axis in the R2 plane. Is that what you are suggesting or am I missing the thread? If so, what does the x axis in the Complex plane represent? – Rasputin Apr 14 '24 at 16:07
  • Suppose you have a map from ${\bf R}^2$ to ${\bf R}^2$, e.g., $f(x,y)=(x^2+y,x+y^2)$. By your logic, ${\bf R}^2$ and ${\bf R}^2$ share both an $x$-axis and a $y$-axis, so you should be able to graph this map in two dimensions. I don't think that's possible. I think you'd need four. – Gerry Myerson Apr 14 '24 at 22:08
  • @GerryMyerson Please ignore if my question is annoying, but your response assumes we are talking about two completely different vector spaces, hence the reference to mapping one vector space onto another. A similar discussion arose here. link where the poster had the same disconnect as me. Why can it simply not be the case that you have one vector space but "one" of the axes in that space happens to be imaginary? That way real and imaginary solutions to a quadratic can all be plotted in one "space". – Rasputin Apr 20 '24 at 14:32

1 Answers1

1

I give a proof over open upward parabola, which can be generalised to open downward parabola too (treat it as exercise!)

Lemma. Let $f(x)=(x+h)^2+k$ be an open upward parabola such that $f(x)=0$ has roots $a\pm bi$, where $a,b\in\mathbb{R}$. Define $g(x):=k-(x+h)^2$, then $g(x)=0$ has roots $a\pm b$.

Proof. By quadratic formula, $$g(x)=0\iff x=\dfrac{2h\pm\sqrt{(-2h)^2-4(-1)(k-h^2)}}{-2}=-h\pm\sqrt{4k}$$ But by $f(x)$, we know $a+bi=\dfrac{-2h\pm\sqrt{(2h)^2-4(h^2-k)}}{2}=-h\pm\sqrt{-4k}$. So we have $$\begin{cases}a=-h\\ b=\sqrt{4k}\end{cases}$$ And it follows that $g(x)=0$ has roots $a\pm b$.

What is the use of this Lemma? The idea is the graph of $g(x)$ is actually obtained by reflecting the graph of $f(x)$ along the horizontal line which touches the vertex of $y=f(x)$. This gives the geometric meaning.

For example, for your $x^2+1$, reflecting the curve $y=x^2+1$ along $y=1$, then it would intersects $x$-axis at $(-1,0)$ and $(1,0)$ so the original function has zeroes $0+1i$ and $0-1i$.

For another example like $x^2+6x+100$, reflecting the curve along $y=100-3^2=91$, you get $91-(x+3)^2$. Then it has the root $$-3\pm\sqrt{91}$$ So $x^2+6x+100=0$ gives the root $-3\pm\sqrt{91}i$.

Hope this answer is useful to you :)

Angae MT
  • 2,206
  • Would you agree with me that it not only needs to be reflected, but rotated 90 degrees? Not sure if you can see my revised diagram or not. – Rasputin Apr 05 '24 at 01:35
  • I guess you need to be more detail. Like the intersection of the rotated curve may not intersect the $z$-axis. And if you transfer the curve rightwards, roots should changed, but the vertical part does not vary. It may not be so obvious after rotated. – Angae MT Apr 05 '24 at 04:19