I calculated the the congruence lattice of $N_5$ using hit and trial and then verified it with Universal Algebra calculator. But I need to prove that it is the congruence lattice of $N_5$ How should I do that?
Given below is the Con Lattice.
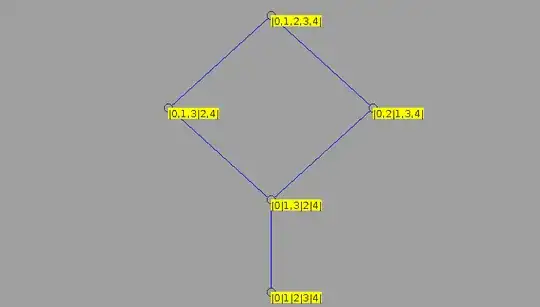
I calculated the the congruence lattice of $N_5$ using hit and trial and then verified it with Universal Algebra calculator. But I need to prove that it is the congruence lattice of $N_5$ How should I do that?
Given below is the Con Lattice.

It looks like your lattice is the congruence lattice of the $N_5$ defined on $\{0,1,2,3,4\}$ with the following relations: $0 < 1 < 3 < 4$ and $0 < 2 < 4$, so the Hasse diagram looks like this:
4
/ \
3 \
| 2
1 /
\ /
0
If you start with this $N_5$, then you can prove the congruence lattice is the one in your picture by considering the congruence generated by (collapsing each of) the intervals in the $N_5$ lattice.
Let $\operatorname{Cg}^{N_5}(x,y)$ denote the congruence generated by (collapsing the pair) $(x,y)$. Check the following:
$\operatorname{Cg}^{N_5}(1,3) = |0|1,3|2|4|$
$\operatorname{Cg}^{N_5}(0,1) =\operatorname{Cg}^{N_5}(0,3) = \operatorname{Cg}^{N_5}(2,4) = \operatorname{Cg}^{N_5}(0,1,3) =|0,1,3|2,4|$
$\operatorname{Cg}^{N_5}(0,2) = \operatorname{Cg}^{N_5}(1,4) = \operatorname{Cg}^{N_5}(3,4) = \operatorname{Cg}^{N_5}(1,3,4) =|0,2|1,3,4|$
If you don't know how to derive these, here's an example derivation:
The pair $(2,4)$ belongs to $\operatorname{Cg}^{N_5}(0,1)$ because $(0,1)$ and $(2,2)$ belong to this congruence, therefore, so must $(0,1)\vee (2,2) = (0\vee 2, 1\vee 2) = (2,4)$.