De-mystifying tricks in proof – If $\{x_n\}$ converges, then Cesaro Mean converges.

Question

Stephen Abbott. Understanding Analysis (2016 2 edn). p. 55. Not a duplicate.

Exercise 2.3.11 (Cesaro Means). (a) Show if $\{x_n\}$ is a convergent sequence, then the sequences given by the averages $\{\dfrac{x_1 + x_2 + ... + x_n}{n}\}$ converges to the same limit. (Not a duplicate)

I rewrote and colored the official solution.

Let $\epsilon>0$ be arbitrary. Then we need to find an $N \in \mathbb{N} \qquad \ni n \geq N \implies\ |\frac{x_1 + x_2 + ... + x_n}{n} - L|< \epsilon \tag{1}$.

Question posits $(x_{n}) \to L$. So $\exists \; M \in \mathbb{N} \ni n \ge M \implies |x_{n}-L|< M \quad (2)$.

$\text{Also } \exists \; C \ni n \ge C \implies |x_{n}-L|< \epsilon/2. \quad \tag{3}$

My question 1. Where does (3) issue from? How to presage $\epsilon/2$? Normally you start with $\epsilon$.

2. Doesn't the same argument prove all the terms can be bounded? Why simply 'the early terms in the averages can be bounded' ? Please expatiate on "Because the original sequence is convergent, we suspect that we can bound ... we will be breaking the limit in two at the end" ?
   I still don't understand how "we suspect" these bounds?

   Now for all $n \ge C$, we can write

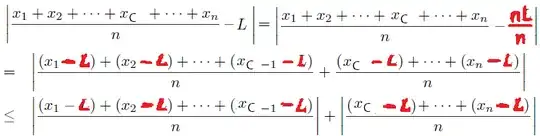
3. How to presage rewriting $\color{red}{L = nL/n}?$

4. How to presage spltting the sum between $x_{C - 1}$ and $x_C$?

   Now apply the Triangle Inequality to each of the $n$ $(x_i - L)$ terms.

   $\begin{align} \le & \frac{1}{n}( & \color{green}{\left| x_{1}-L\right| +\ldots +\left| x_{c-1}-L\right|} & + \color{brown}{\left| x_{C}-L\right| +\ldots +\left| x_{n}-L\right|} & )\\ & & \color{green}{\text{Each of these $(C - 1)$ terms < M by (2)} } & \color{brown}{ \text{ Each of these $(n - C)$ terms < $\epsilon/2$ by (3)}} & \\ \le & \frac{1}{n}( & \color{green}{(C - 1)M} & + \color{brown}{\frac{e}{2}(n - C)} & ). \tag{4}\\ \end{align}$

5. Why is the last inequality (4) above $\le$? Why not $<$ like (2) and (3)?

   Because C and M are fixed constants at this point, we may choose $N_2$ so that $\color{green}{(C - 1)M}\frac{1}{n} < e/2 \tag{5}$ for all $n \ge N_2$. Finally, let $N$ [in $(1)$] $= \max\{C, N_2\}$ be the desired $N$.

6. Why are we allowed to choose $N_2$ so that $\color{green}{(C - 1)M}\frac{1}{n} < e/2$?

   $C \in \mathbb{N} \quad \therefore n - C < n \iff \color{magenta}{\frac{n - C}{n}} < 1 \tag{6}$

   $\begin{align} \text{Equation (4) is} & & \color{green}{(C - 1)M}\frac{1}{n} & + \frac{e}{2}\color{magenta}{\frac{n - C}{n}}. \\ \text{Then by (5) and (6),} & & < e/2 & + e/2\color{magenta}{(1)}/ QED. \\ \end{align}$

Answer 1

1. Where does (☺) issue from? Did solution rewrite M in (♪) as C? How to presage $e/2$ ?
Cesaro means is $\dfrac{a_1 + ... + a_n }{n }$. n is fixed. Ergo how can we choose $K$? And what's $l$?
1.1. Your 2e last sentence : " we can bound the later terms using the convergence of the $\color{Red}{regular}$" I don't understand. Should there be words after $\color{Red}{regular}$?

Both (☺) and (♪) come from the definition of the limit. The usage of $C$ corresponds to the upper bound $e/2$, while $M$ is used for the upper bound $M$. To presage $e/2$, consider that for any fixed sum $\dfrac{a_1+\dots+a_\ell}{K} \leq \dfrac{\ell}{K}\max_i(a_i)$, we can choose $K$ to make the fraction arbitrarily small. Here $\ell$ is an arbitrary index chosen so as not to be involved in the problem directly. For any $\varepsilon>0$ if we choose $\dfrac{l}{K} < \varepsilon \iff K>\ell/\varepsilon$, then the sum $\dfrac{a_1+\dots+a_\ell}{K} <\varepsilon$. Hence, the early terms in the averages can be bounded. Because the original sequence is convergent, we suspect that we can bound the later terms using the convergence of the regular sequence (the word sequence was omitted in an earlier edit by mistake). Hence, we suspect that we will be breaking the limit in two at the end, so we will want $e/2$ for bound.

As a note, if I were writing the proof, I would write the proof with all my bounds $\eta$ and then choose $\eta$ to make the conclusion match the arbitrary $\epsilon$.

2. How to presage feyly to rewrite $\color{red}{L = nL/n}?$
I know question posits $\{x_n\}$ is a convergent sequence.
But I'm nonplussed why 'we would like to compare each term to the limit' ?

We should compare the sequence to the limit because that is the only number to which a meaningful comparison can be made. The sequence may behave arbitrarily with the exception that it converges to some limit $L$.

As we saw in the first part, we suspect that we should break the sum into two parts. Because the sequence is convergent, we would like to compare each term to the limit. To do so we use the rules of algebra to put $L$ on a common denominator, or equivalently, write $nL/n$.

3. How to presage presciently to split the sum between $x_{C - 1}$ and $x_C$ ?

Continuing the argument from the first part, we break the sum into two pieces at an arbitrary point $C$. Then we simplify the fractions, and bound them using the technique from part 1.

4. I know we want the bound to behave, but what or who sanctioned us to choose $N_2$ and to invoke $\color{green}{(C - 1)M}\frac{1}{n} < e/2$? We can't just choose whatever we want?

Because we want the result to be true in the limit we must show that for all sufficiently large $n$, the bound holds. We choose $N_2$ to make the fraction resulting from the early terms of the series small. The number $N_2$ is an arbitrary number, with the only requirement that it be large enough to guarantee that the fraction is sufficiently small.

5. Shouldn't this last line start with $<$?

If you are referring to the line given by the triangle inequality, then we must put '$\leq$' because that is all the triangle inequality gives. The next line is strict inequality for appropriate choices of $M$ and $C$.