Let $G$ be a finite simple undirected graph. Suppose we contracted some edges of $G$ to form a new graph $G_1$. Then, is it true that the genus of $G$ is greater than or equal to the genus of $G_1$?
Thanks in advance.
Asked
Active
Viewed 546 times
3
-
Isn't this sort of obvious from a picture? (It is enough to consider the case in which one edge is contracted) – Mariano Suárez-Álvarez Feb 03 '14 at 06:16
-
Do you mean that the result is true and it is obvious from a picture? – D. N. Feb 03 '14 at 06:19
-
@MarianoSuárez-Alvarez: Just being curious - I'm not an expert in graph theory, but is it possible to prove that the genus of $G$ is greater than or equal to the genus of $G_1$ using mathematical methods? – Feb 03 '14 at 06:19
-
@D.N., indeed. ${}$ – Mariano Suárez-Álvarez Feb 03 '14 at 06:20
-
@SanathDevalapurkar, I don't understad what is unmathematical in my suggestion. The argument from a picture can obviously be formalized, provided a corresponding formalization of what the genus of a graph is, and given enough motivation. – Mariano Suárez-Álvarez Feb 03 '14 at 06:22
-
@MarianoSuárez-Alvarez. Thank you so much. – D. N. Feb 03 '14 at 06:29
1 Answers
4
A picture:
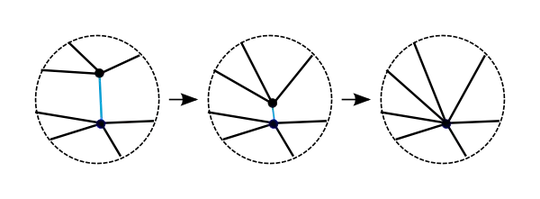
Given an embedding of a graph on a surface, fix an edge and look at the piece of surface near it. If the chosen edge is the blue one, then the circles above show the piece of the surface near it. Then shrink the edge until it is gone, and adjust the embedding along the way. You end up with an embedding of the contracted graph in the same surface.
An animated variant:
Mariano Suárez-Álvarez
- 139,300
-
How could doing the reverse, splitting a vertex into two with an edge in between, potentially affect the genus? Maybe more specifically, what if we split a vertex with valence 4 and split it so each of the two vertices has valence three. – user2154420 Jul 01 '14 at 15:12