I'm prepping for the GRE.
Would appreciate if someone could explain the right way to solve this problem. It seems simple to me but the site where I found this problem says I'm wrong but doesn't explain their answer. So here is the problem verbatim:
Find the number of paths from x to y moving only right (R) or down (D).
My answer is 6. What am I missing??
Thanks for any help.
The solution to the general problem is if you must take $X$ right steps, and $Y$ down steps then the number of routes is simply the ways of choosing where to take the down (or right) steps. i.e.
$$ \binom{X + Y}{X} = \binom{X + Y}{Y} $$
So in your example if you are traversing squares then there are 5 right steps and 1 down step so:
$$ \binom{6}{1} = \binom{6}{5} = 6 $$
If you are traversing edges then there are 6 right steps and 2 down steps so:
$$ \binom{8}{2} = \binom{8}{6} = 28 $$
If you panic during the test, consider just drawing it as a Pascal's triangle
Where
Any such path is a permutation of 6 R and 2 D, so the answer is $${6+2\choose 2}={8\choose 2}=\frac{{8 \times 7}}{2}=28$$
To get from point x (not square x) to point y there are $8$ steps to be taken. $2$ of them downwards and $6$ to the right. So it just comes to electing exactly $2$ of the $8$ consecutive steps to be the steps downwards.
Picking $2$ out of $8$ can be done on $\binom{8}{2}=28$ ways.
When you are thinking in squares instead of points then there $6$ steps to be taken. $1$ of them downwards and $5$ to the right. So it just comes to electing exactly $1$ of the $6$ consecutive step to be the steps downwards.
Picking $1$ out of $6$ can be done on $\binom{6}{1}=6$ ways.
That explains the fact that your answer was $6$.
See here you can easily compute the number of paths by applyinfg the COMBINATION concept.
So what is the concept!!
ok then.....let us consider to proceed from x to y we have to take the steps to the direction of RIGHT and DOWN....fine?
and let us take RIGHT = R and DOWN = D.....still fine.. :-)
now see if anyone wants to go from X to Y he must take 2 DOWN steps and atmost 6 RIGHT step.
So we can say that we have to take total 8 numbers of step.You can check it by your own that we must take 8 steps to reach at Y starting from X poit.ok.
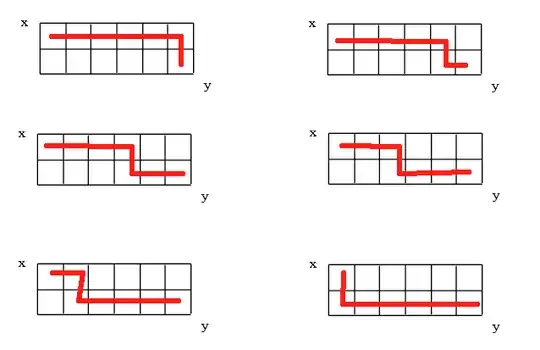
and see here we can write a combination of steps,like: { R-R-R-R-D-R-D-R } -----(see its a suitable traverse path.match this path with the picture.)
And now we can make our main observation on this problem.....So what is it? See, you have to take total of 8 steps and all of them are the combination of R and D's ok?
And the observation is: You have to take just 2 D(DOWN step) and also just 6 R(RIGHT step) to reach at Y.
So we can say that the total number of combination is: HOW MANY COMBINATION OF 'R' OR 'D' is possible from the total of 8 steps!!!!!
The required answer is actually the combination of 2 PLACES for D's OR 6 PLACES for R's from 8 total steps(OR TOTAL 8 PLACES where R and D letters take place)........
see here we are just mapping our problem of counting the number of suitable paths from X to Y into a basic counting problem.....And we just logically made a connection between these two problems and it is clear that if we can calculate the combination of 2 PLACES for D's OR 6 R's from total 8 steps it will be enough!!
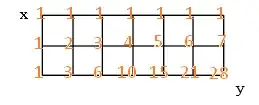
Here is the total of 8 places where D and R may take places:
{ ___ ___ ___ ___ ___ ___ ___ ___ }
And we actually CHOOSE 2 places for for 2 D's OR we CHOOSE 6 places for 6 R's but we dont bother for the oreding of D's OR R's.....the 2 D's OR the 6 R's can tale place randomly but their requirement for the places is fixed!! it is 2 for 2 D's and it is 6 for 6 D's......actually choosing 2 D's OR 6 R's are basically same!! :-)
So, the answer is : 8C2 or 8C6 (note that both are same!! :-) ) 8C2 = 28 and easily you can see 8C6 = 28.
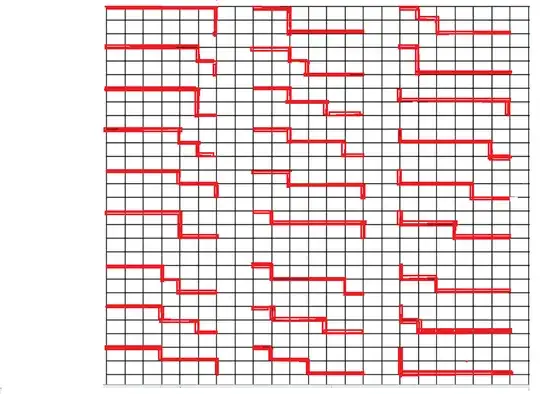
SO, THERE ARE 28 PATHS FROM X TO Y!!
$\newcommand{\+}{^{\dagger}}% \newcommand{\angles}[1]{\left\langle #1 \right\rangle}% \newcommand{\braces}[1]{\left\lbrace #1 \right\rbrace}% \newcommand{\bracks}[1]{\left\lbrack #1 \right\rbrack}% \newcommand{\ceil}[1]{\,\left\lceil #1 \right\rceil\,}% \newcommand{\dd}{{\rm d}}% \newcommand{\down}{\downarrow}% \newcommand{\ds}[1]{\displaystyle{#1}}% \newcommand{\equalby}[1]{{#1 \atop {= \atop \vphantom{\huge A}}}}% \newcommand{\expo}[1]{\,{\rm e}^{#1}\,}% \newcommand{\fermi}{\,{\rm f}}% \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,}% \newcommand{\half}{{1 \over 2}}% \newcommand{\ic}{{\rm i}}% \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow}% \newcommand{\isdiv}{\,\left.\right\vert\,}% \newcommand{\ket}[1]{\left\vert #1\right\rangle}% \newcommand{\ol}[1]{\overline{#1}}% \newcommand{\ot}{\downarrow}% \newcommand{\pars}[1]{\left( #1 \right)}% \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}}% \newcommand{\root}[2][]{\,\sqrt[#1]{\,#2\,}\,}% \newcommand{\sech}{\,{\rm sech}}% \newcommand{\sgn}{\,{\rm sgn}}% \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\ul}[1]{\underline{#1}}% \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert}$ In general we have steps to right and down. Tipically, this is a possible path: $$ {\Huge \to\ \to\ \down\ \to\ \to\ \to\ \down \to} $$ In general, the problem is reduced to put two down arrows $\down$ in 8 sites like the following example: $$ \begin{array}{cccccccc} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ &&&&\down&&\down \end{array} $$ Let's put one $\down$ at the first step, then we have $\color{#ff0000}{\large 7}$ positions left to put the other one. Next, we put the first $\down$ at the second step and we have $\color{#ff0000}{\large 6}$ position left to put the other one and so on such that $7 + 6 + 5 + 4 + 3 + 2 + 1 = \color{#0000ff}{\Large 28}$ which is $\ds{8 \choose 2}$.
Check this handcrafted portable network graphic :
First note that you will always be moving 6 squares right and 2 squares down, just because $y$ is 2 squares down and 6 squares to the right from $x$.
Next, note that a different ordering of these steps will always result in a different path. Then, the question simply becomes how many ways there are to arrange 6 "right steps" and 2 "down steps" from first to last.
This is equal to the total number of ways to arrange 8 steps ($= 8!$), divided by the number of different ways that are accounted for by some of the steps being the same ($6!$ for 6 right steps and $2!$ for 2 down steps), which is $\displaystyle \frac{8!}{6!2!} = 28$.
If you're moving only 5 squares right and 1 square down, which is the case if you're moving on the insides of squares rather than the intersections of grid lines, then you're arranging 6 total steps, 5 right and 1 down, which gives the formula $\displaystyle \frac{6!}{5!1!} = 6$.
Others have come up with similar alternative solutions but I'll try to be more concise:
PS.
To get the logic of number of reordering of letters, try to play with simple words such as $dog$, $doggy$, $moon$.
I believe you have $28$ ways really. I give you $27$ and try to find out the only absent in the figure below
i see alot of good explanations but in my opinion the most useful and simple answer is for any nxm matrix using the down or right rule there are $${(n-1)+(m-1)\choose(m-1)}$$ paths.
Well you can do only down and right($6$ right and $2$ down)
Now if we show the way we get to $8$ digit word that has $2$ and $6$ similers
We can change the place of $8$ digits to make $8!$ different words.But there are duplicate cases the similar $6$ digits can be change without making any new words that we should divide the answer to $6!$also that two similar digits can changed without making any new words which means we should also divide it by $2!$ which gives:
$\frac{8!}{6!2!}=\frac{56}{2}=28$
28 is the answer. As,from x to y,there are 2 downward steps and 6 horizontal,rightward steps, so,going by the general formula
***{(m+n)!}/{(m!n!)}***
=>{(2+6)!}/{2!6!}
=>{8!}/{2!6!}
=>**28**
Hence,this is the required answer.
