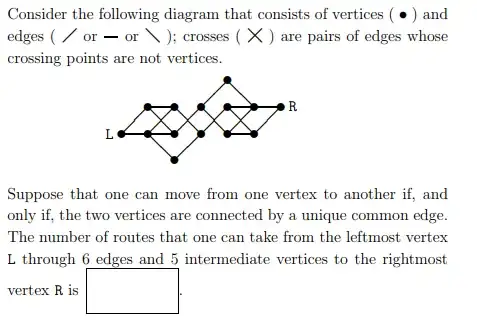
I am currently studying for the MEXT exam (an underdrag math exam for people seeking to studying in Japan with a MEXT Scholarship) and meanwhile I understand most questions I do not know how to approach this one at all. Can someone give me some tips or advice on how to approach this question or what to study in order to answer it? Thanks.
I've seen this sort of problem in combinatorics. A similar problem is here: Calculating the number of possible paths through some squares .
For this particular problem, the constraint of a path through $5$ vertices and $6$ edges requires that the path always move to the right. Starting at the vertex labelled "$L$", label it as having one (always advancing to the right) path to it : start at $L$ and don't move. Then for each column of vertices, in left-to-right order, label each vertex with the sum of the labels on the vertices which share an edge to it in the previous column.
The second column has two vertices. Both have an edge (and only that edge) to the vertex labelled "$L$", so both are labelled "$1$".
The third column has three vertices. The top vertex has two neighbors to its left, both labelled "$1$", so it is labelled "$2$". The middle vertex has two neighbors to its left, both labelled "$1$", so it is labelled "$2$". The bottom vertex is adjacent to one vertex to its left, labelled "$1$", so it is labelled "$1$".
Notice that the labels keep track of the number of ways to reach that vertex starting at $L$ and advancing always to adjacent edges to the right. When we reach the column containing $R$, we label it with the number of paths from $L$ to $R$ advancing always to the right. As we initially noted, these are the paths through $5$ vertices and $6$ edges, so is exactly the set of desired paths.
