Intuition and Tricks - Hard Overcomplex Proof - Order of Subgroup of Cyclic Subgroup - Fraleigh p. 64 Theorem 6.14

Question

Update Dec. 28 2013. See a stronger result and easier proof here. I didn't find it until after I posted this. This isn't a duplicate. Proof is based on ProofWiki. But I leave out the redundant $a$.

Let $\color{magenta}{\langle {g} \rangle \text{ be the cyclic group of order } n}$ generated by $g$. Let $g^i \in \langle {g} \rangle$. Then $\left|{\langle {g^i} \rangle }\right| = \frac n {\gcd \left\{{n, i}\right\}}$.

Proof: Subgroup of Cyclic Group is Cyclic says $\langle {g^i} \rangle$ is cyclic.
We need to show that $\langle {g^i} \rangle$ has $n / gcd(n, i)$ elements. Let $\left|{\langle {g^i} \rangle}\right| = k$.
Hence by Non-Trivial Group has Non-Trivial Cyclic Subgroup, $(g^i)^k = e$. Hence $ (g^i)^k = e \color{magenta}{ = g^n}$. Pinter p. 104 Theorem 5 says 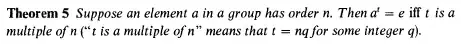Hence $\color{magenta}{n} | ik$.

We now need to calculate the smallest $k$ such that $n \mathop \backslash i k$.
That is, the smallest $t \in \mathbb{N}$ such that $n t = i k$. Thus $t = \dfrac{ik}{n} = \dfrac {ik\color{blue}{{\dfrac{1}{gcd(n, i)}}}}{n\color{blue}{\dfrac{1}{gcd(n, i)}}} = k\dfrac {{\dfrac{i}{gcd(n, i)}}}{\dfrac{n}{gcd(n, i)}}$

From Divide by GCD for Coprime Integers, $\frac{n}{gcd(n, i)}$ and $\frac{i}{gcd(n, i)}$ are coprime.

Thus from Euclid's Lemma, $\frac{n}{gcd(n, i)} \mathop \backslash k$.

For all $a,b, a \mathop \backslash b \implies a \le b$. Hence the smallest $k$ such that $k/{\frac{n}{gcd(n, i)}} \in \mathbb{Z}$ is $n / d$.

1. How do you envisage and envision $\left|{\langle {g^i} \rangle }\right| = \frac n {\gcd \left\{{n, i}\right\}}$ before doing the proof?

2. Why do we need to calculate the smallest $k$ such that $n \mathop \backslash i k$?

3. How do you envisage and envision to multiply top and bottom by $\color{blue}{\frac{1}{gcd(n, i)}}$? Magic?
4. The last line talks about smallest $k$ such that $k/{\frac{n}{gcd(n, i)}}$. Why do we need this?
   And how can you envisage and envision we needed this?

Answer 1

Here is a simple way to conceptualize the proof. First we shift from multiplicative to additive language. Thus, in $\,\Bbb Z/n,\,$ we seek the order of $\,i,$ or, equivalently, the order (size) of the subgroup $H$ that it generates. The integers congruent to elements of $\,H = \langle i\rangle$ are precisely those of form $ki + jn$ for some $k,j\in \Bbb Z.\,$ By Bezout, these are precisely all multiples of their gcd $\,(i,n),\,$ i.e.

$$ \exists\, k\!:\ x \equiv k\,i\!\!\pmod{\! n} \iff \exists\, k,j\!:\ x = k\,i+j\,n \iff (i,n)\mid x\qquad$$

So the elements of $H$ are precisely the multiples of $\,d = (i,n),\,$ in $\,\Bbb Z/n,\,$ of which there are $\,n/d.$

Remark $\ $ Alternatively one may use the universal $\rm\color{#0a0}{(U)}$ and distributive $\rm\color{#c00}{(D)}$ laws of the gcd:

$${ki\equiv0\!\!\!\pmod{\! n} \iff n\mid ki \iff n\mid ki,kn\!\!\! \color{#0a0}{\overset{\rm\,\ (U)}{\iff}}\!\! n\mid (ki,kn)\color{#c00}{\overset{\rm(D)}=}k(i,n) \iff n/(i,n)\mid k}$$

Answer 2

For (1), I think the intuition is the following. Let $a=g^i.$ If $i\mid n,$ then $n=is,$ $\langle a\rangle=\{e,g^i,g^{2i},\ldots,g^{i(s-1)}\},$ and things are very simple since $\langle a\rangle$ has order $s=n/i.$ Now if $i\nmid n$, you try to imagine what powers of $g$ occur in the list $e,g^i,g^{2i},\ldots$ For $j$ big enough, $ji$ will be bigger than $n.$ But then $g^{ji}$ will be the same as $g^{ji-n}.$ Furthermore, the inverse of $g^i$ will be $g^{-i}=g^{n-i}.$ Thinking about it some more, you realize you will be able to form arbitrary powers of the form $g^{ai+bn}=g^{ai}$ with $a$ and $b$ integers (positive, negative or zero). If you've ever played with the Euclidean algorithm, you will know that $ai+bn$ is always divisible by $\gcd(i,n)$ and that, by choosing the right $a$ and $b,$ you can write $\gcd(i,n)$ itself in this form. But then $\langle a\rangle$ is generated by $g^{\gcd(i,n)}$ just as well as by $a$ itself, and you are in the first case since $\gcd(i,n)\mid n.$

For (2), you know that $g^{ik}=e,$ where $k$ is the order of $\langle a\rangle.$ So by the Theorem $5$ that you quote, you know that $ik$ is a multiple of $n.$ But if $g^{ik}=e,$ then $g^{2ik}=e,$ $g^{3ik}=e,$ and so on. So it is not the case that if $g^{ik}=e,$ you can conclude that $k$ is the order of $\langle a\rangle.$ It might be that $k$ is a multiple of $\lvert\langle a\rangle\rvert.$ Since we are trying to find $\lvert\langle a\rangle\rvert,$ we don't want one of these multiples—we want the least $k$ for which $g^{ik}=e,$ that is, the least $k$ for which $ik$ is a multiple of $n.$

In (3), we are trying to find this least $k.$ But then the multiple of $n$ that $ik$ is equal to is also least. We are trying to find this least $t$ such that $ik=tn.$ Writing $t=ik/n=(i/n)k,$ we see that $t$ is a certain fraction times $k.$ Dividing $i$ and $n$ by $\gcd(i,n)$ reduces this fraction to lowest terms. This is helpful since, if $a/b$ is in lowest terms, and if $(a/b)k$ is an integer, then $b$ must divide $k.$ If $a/b$ isn't in lowest terms, we won't be able to conclude this, since you can also get an integer by having some of the factors of $b$ cancel with $a$ and others with $k.$ By reducing to lowest terms, you guarantee that all factors of $b$ cancel with $k.$ Since our $b$ is $n/\gcd(i,n),$ we know that $k$ is divisible by $n/\gcd(i,n).$

To get the conclusion, we need to show that $k$ actually equals $n/\gcd(i,n).$ Remember that $k$ is the least natural number such that $ik$ is divisible by $n.$ We know that $k$ is a multiple of $n/\gcd(i,n).$ The least multiple of a number is that number itself. Would that work here? The answer is yes since then $ik=in/\gcd(i,n).$ As $i/\gcd(i,n)$ is a positive integer, we see that $ik$ is indeed a multiple of $n.$

Answer 3

Here are a few remarks on your questions.

1. When you are considering $\vert\langle a\rangle\vert$ you know that this is going to be a factor of $n$ (for example as $\langle a\rangle\leq\langle g\rangle$ and then use Lagrange's Theorem), so you know that $\vert\langle a\rangle\vert=\frac{n}{??}$. To determine what the denominator is, you have to think about how many times you have to cycle round with $a=g^{i}$ to get a power of $g^{n}=e$. If you write $i=\alpha\cdot gcd(n,i)$ and $n=\beta\cdot gcd(n,i)$, you will have that $\alpha$ and $n$ are coprime (so $gcd(\alpha,n)=1$). Thus you can get a multiple of $i$ to be equal to a multiple of $n$ by multiplying by $\beta$ as \begin{align*} i\cdot \beta=\alpha\cdot gcd(n,i)\cdot \beta=\alpha\cdot n. \end{align*} But as $gcd(\alpha,n)=1$, you see that $gcd(n,i)$ is the least value you can take.
2. See part 1.
3. You are trying to simplify the fraction $\frac{ik}{n}$. The only thing you really know is that the numerator and denominator are divisble by $gcd(ni)$, hence you get the result.
4. You want to find the smallest $t\in\mathbb{N}$ such that \begin{align*} t=k\frac{(i/gcd(n,i))}{(n/gcd(n,i)}. \end{align*} Thus you want to minimise the value of \begin{align*} k\frac{(i/gcd(n,i))}{(n/gcd(n,i)}. \end{align*} However, as $i/gcd(n,i)$ and $n/gcd(n,i)$ are coprime, we must have that $n/gcd(n,i)$ divides $k$. Thus to minimise $t$, you want the smallest $k$ such that $(n/gcd(n,i))$ divides $k$.