6

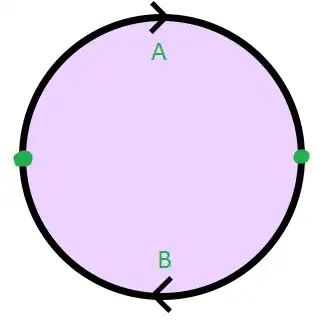
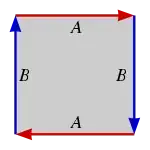
Wikipedia gives the following fundamental polygon for the real projective plane $\mathbb{R}\mathrm{P}^2$ Fundamental polygon

The problem here is that the corners aren't identified to a single point (like in the fundamental polygon of the torus). I don't think this picture is correct. The group presentation resulting from this polygon was considered in a previous question, and the same conclusion was reached.

What puzzles me more is that Hatcher's Algebraic Topology lists the same polygon as the fundamental polygon for the real projective plane (chapter 2, page 102), but the correct version (with only two edges identified together) is listed in an earlier page (chapter 1, page 51).

My question: Can this fundamental polygon made to actually represent the real projective plane in the sense that all corners are identified to a point and the resulting group presentation is $\mathbb{Z}_2$?

Thank you.

Community
  • 1
PeterM
  • 5,661
  • For a torus, all four corners are the same point, but here, each pair of opposite corners can be identified. – Victor Liu Oct 24 '13 at 23:46

1 Answers1

3

If you're ok with the fundamental polygon being a polygon on a surface which isn't $\mathbb{R}^2$, then you can get a polygon with two edges on the sphere $S^2$.

The polygon is given by taking the northern hemisphere, and the edges are given by each a half of the equator, with the identification being the antipodal map on the circle defining the equator.

enter image description here

If you know how covering spaces work, this region is a fundamental region of the $2$-fold covering of the sphere on to the real projective plane.

Dan Rust
  • 30,973
  • I figured out what my problem was. Both fundamental polygons give the real projective plane, but the one in Wikipedia cannot be used to compute the fundamental group using the theorem in question because it doesn't give a wedge sum of circles with a 2-cell attached. – PeterM Oct 29 '13 at 22:20
  • Using the fundamental polygon you gave in the question, you'll notice that the boundary of the punctured real projective plane is generated by the loop you get by concatenating $A$ and $B$, and so in terms of Van Kampen's theorem, you have $$\pi_1\mathbb{R}P^2\cong (\langle AB\rangle\ast 1)/\langle ABAB\rangle\cong\langle AB\mid ABAB\rangle\cong\langle x\mid x^2\rangle\cong\mathbb{Z}_2$$ – Dan Rust Oct 29 '13 at 22:35