Proof by Math Induction

Question

I have 3 math induction proofs I have been struggling with for a while. I understand how to do summation proofs but these ones, I can't find a general pattern to solve. Please help.

1) $D(n) = {n(n-3) \over2}$ for all $n \ge 3$ This is for the n diagonals of a polygon.

2)$\binom{n}{0} + \binom{n}{1} + \binom{n}{2} + \ldots + \binom{n}{n} = 2^n$ for all $n\ge 0$

3)$n^2 + 1 \ge 3n$ for all $n \ge 3$; For this one, I got stuck when I did this:

$$\begin{align} k^2 + 1 &\ge 3k \\ (k+1) ^ 2 +1 &\ge 3(k+1) \\ (k+1) ^ 2 &\ge k^2 \ge 3k \\ (k+1) ^ 2 &\ge k^2 + 3 \ge 3k + 3 \,\, \text{(? I don't know how to proceed from here ?)} \end{align}$$

Please give me possible solutions and techniques to solve these kind of problems.

Answer 1

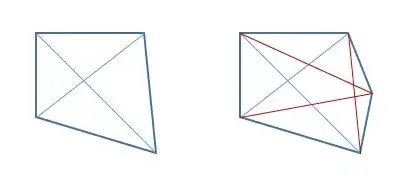
I assume that $D(n)$ is the number of diagonals in an $n$-sided convex polygon. Descriptively: each vertex of the polygon can be connected to $n-3$ other (connecting it with itself or its neighbors will not produce diagonals). That way, you make each diagonal twice, hence the formula.

If you want to use induction, then check for $n=3$, and then assume it works for all $k$-sided convex polygons where $k < n$. Look at the $n$-sided one.

We can pick any $n-1$ vertices, and the polygon they span has $(n-1)((n-1)-3)/2$ diagonals (by the assumption). But, one of its sides will also become a diagonal of the bigger polygon. Now, we're just missing $n-3$ diagonals from the $n$-th vertex, so in total we have:

\begin{align*} \frac{(n-1)((n-1)-3)}{2} + 1 + (n-3) &= \frac{(n-1)(n-4) + 2 + 2(n-3)}{2} \\ &= \frac{n^2 - 5n + 4 + 2 + 2n - 6}{2} = \frac{n^2 - 3n}{2} \\ &= \frac{n(n-3)}{2}. \end{align*}

If you want the second one using induction, use the recursive formula for binomial coefficients:

$$\binom{n}{k} = \binom{n-1}{k-1} + \binom{n-1}{k}.$$

Edit: Since you asked how to do this (in comment to nsanger), I'm expanding that part of the answer. The idea is to note that the two terms on the right hand side are the same, only with a shift in $k$. In other words:

$$\sum_{k=1}^n \binom{n-1}{k-1} = \sum_{k=\color{red}{0}}^{\color{red}{n-1}} \binom{n-1}{\color{red}{k}}.$$

Now, we just need to play with the edge cases to get the sums to have the same limits: \begin{align*} \sum_{k=0}^n \binom{n}{k} &= \binom{n}{0} + \binom{n}{n} + \sum_{k=\color{red}{1}}^{\color{red}{n-1}} \binom{n}{k} = 1 + 1 + \sum_{k=1}^{n-1} \binom{n-1}{k} + \sum_{k=1}^{n-1} \binom{n-1}{k-1} \\ &= \binom{n-1}{0} + \sum_{k=1}^{n-1} \binom{n-1}{k} + \binom{n-1}{n-1} + \sum_{k=1}^{n-1} \binom{n-1}{k-1} \\ &= \sum_{k=\color{red}{0}}^{n-1} \binom{n-1}{k} + \sum_{k=1}^{\color{red}{n}} \binom{n-1}{k-1} \\ &= \Big\{ \text{Use the above formula for the second sum} \Big\} \\ &= \sum_{k=0}^{n-1} \binom{n-1}{k} + \sum_{k=0}^{n-1} \binom{n-1}{k} = 2\sum_{k=0}^{n-1} \binom{n-1}{k} \\ &= \Big\{ \text{Use the induction hypothesis} \Big\} \\ &= 2 \cdot 2^{n-1} = 2^n. \end{align*}

The third one was answered by nsanger, so I won't be repeating that.

Answer 2

I don't know what the function $D(n)$ is, so I can't help you on the first problem.

To prove the second equality you don't actually need induction, you can just use the binomial theorem, which states that $$(a+b)^n=\sum_{k=0}^n \binom{n}{k}a^{n-k}b^k$$ If you plug in $a = b = 1$ then you are left with $$2^n = (1+1)^n=\sum_{k=0}^n\binom{n}{k}1^{n-k}1^{k}=\sum_{k=0}^n\binom{n}{k}=\binom{n}{0}+\binom{n}{1}+\binom{n}{2}+\cdots+\binom{n}{n}$$

To prove the third one by induction, first note that in the case $n = 3$ you have $n^2 + 1=10>9=3n$, so the theorem holds for the base case. To prove it for the $n+1$ case, since you are given that $n^2 + 1 > 3n$, and that $n\geq 3$, you can say that $2n +1> 3$ so therefore $$n^2+1>3n\implies (n^2+1)+(2n+1)>3n+3$$ $$(n^2+2n+1)+1>3(n+1)$$ $$(n+1)^2+1>3(n+1)$$ which shows the theorem holds for the $n+1$ case as well, concluding the proof.

Answer 3

1) The base case is a triangle, having no diagonal. Then take a polygon of $n$ vertices, add a vertex on an edge and displace it. This makes $n-1$ new diagonals appear ($n-2$ to the new vertex plus the original edge). This matches $D(n+1)-D(n)=n-1$.

2) The base case $n=0$ is trivial, $2^0=1$. Now take a row in Pascal's triangle. You know that it is obtained by adding pairwise the elements of the previous row. So the sum of the row is twice that of the previous row.

3) The base case is true, as $10\ge9$. Then subtract memberwise the inequalities for $n+1$ and $n$ (don't forget to swap the sides): $$\begin{align} &(n+1)^2+1&\ge&3(n+1)\\ -\ \ \ \ \ \ &n^2+1&\ge&3n\\ =\ \ \ \ \ \ &n^2-n+2&\ge&-n^2+3n\\ \end{align}$$

The last relation can be rewritten $2(n-1)^2\ge0$, which is always true.