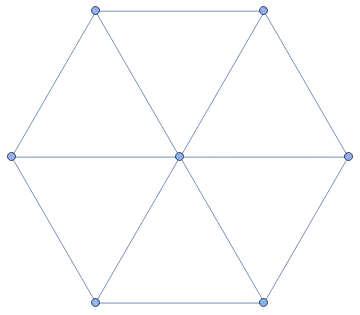
I am looking for a constructive classification of those finite, simple graphs (no loops, no multi-edges), where the open neighbourhood of each vertex (excluding that vertex aka open neighbourhood) is isomorphic to $C_6$; equivalently, where the closed neighbourhood of each vertex including that 'central' vertex is isomorphic to the wheel graph $W_7$ with 6 spokes
Alternatively, theses graphs are called 'locally $C_6$ (open)'.
Well, I thought this would be straightforward, construct a cylinder and glue it in various twisted ways to find the torus and Klein bottle graphs (constructions 1 and 3 below)...
I was surprised to find -actually in Mathematica's graph data- that many 'locally $C_6$' graphs can only be constructed differently as per below; NB though, that for selected parameters, these constructions are redundant and the same graph can be constructed with different constructions.
My question is
which 'locally $C_6$' graphs do I miss and which constructions do I miss?
BTW: I can't find the sequence of the number of 'locally $C_6$' graphs in OEIS for $v$ vertices ($v\geq 12$ up to $25$): 1, 1, 2, 1, 6, 1, 3, 2, 8, 3, 4, 2, 12, 5 ...
BTW2: I understand that there should be some link to the classification of finite groups and boundary mappings of the fundamental domains of these graphs in a triangular tiling of the plane but I have not been able to make that explicit... Please share, if you have a good reference on that.
BTW3: I am aware of this paper https://arxiv.org/abs/math/0512332 on 'Hexagonal Tilings and Locally C6 Graphs' by Garijo etal but I can't quite make sense of all constructions for hexagonal tilings and then how to transfer them to the $C_6$ case.
Current constructions
- 'Classic' Klein bottle: Take a cylinder (you have a natural direction around), then glue the 2 ends in a way that this natural direction is broken
- 'Figure 8' Klein graph: Take a cycle graph with an even number of vertices; take it double (so that you have a pretzel); as seen fit, build a cylinder; close off the ends by gluing to another cycle graph with half the number of vertices
- 'Twisted torus': Take a cylinder and glue it in a way that preserves the direction but twist it before gluing resulting in different graphs
- Combinatorial constructions: Start from a cycle graph numbered in increasing order and link each point $j$ with $j+k_1$ and $j+k_2$
In Mathematica
cyl[jj_, kk_] := MapApply[UndirectedEdge,Map[Sort,Join[ Flatten[ Table[ { {{j, k}, {Mod[j+1,jj,1], k}}, {{j, k}, {j, k+1}}, {{j, k}, {Mod[j+1,jj,1], k+1}} }, {j,1,jj}, {k,1,kk-1}], 2], Flatten[Table[ { {{j, kk}, {Mod[j+1,jj,1], kk}} }, {j,1,jj}], 1] ]]];
kgraph[jj_,kk_] := Union[Join[ cyl[jj,kk], MapApply[UndirectedEdge, Map[Sort, Flatten[ Table[{{{j,1},{Mod[-j,jj,1],kk}},{{j,1},{Mod[-1-j,jj,1],kk}}}, {j,1,jj}] ,1]]] ]];
k2graph[jj_,kk_,sec_] := Join[ cyl[jj,kk-1], MapApply[UndirectedEdge, Map[Sort, Flatten[ Table[{
{{Mod[j,sec,1],0},{Mod[j+1,sec,1],0}},
{{Mod[j,sec,1],0},{Mod[j,jj,1],1}}, {{Mod[j,sec,1],0},{Mod[j+sec,jj,1],1}},
{{Mod[j,sec,1],0},{Mod[j+1,jj,1],1}}, {{Mod[j,sec,1],0},{Mod[j+1+sec,jj,1],1}}, {{Mod[j,sec,1],kk},{Mod[j+1,sec,1],kk}},
{{Mod[j,sec,1],kk},{Mod[j,jj,1],kk-1}}, {{Mod[j,sec,1],kk},{Mod[j+sec,jj,1],kk-1}}, {{Mod[j,sec,1],kk},{Mod[j+1,jj,1],kk-1}}, {{Mod[j,sec,1],kk},{Mod[j+1+sec,jj,1],kk-1}}}, {j,1,sec}] ,1]]] ];
tgraph[jj_,kk_,tw_] := Join[ cyl[jj,kk], MapApply[UndirectedEdge, Map[Sort, hh=Flatten[ Table[{{{j,1},{Mod[tw+j,jj,1],kk}},{{j,1},{Mod[-1+tw+j,jj,1],kk}}}, {j,1,jj}] ,1]]] ];
cgraph[jj_, kk_, ll_] := Union[MapApply[UndirectedEdge, Map[Sort, Flatten[ Table[ {{j, Mod[j+1,jj,1]}, {j, Mod[j+kk,jj,1]}, {j, Mod[j+ll,jj,1]}}, {j,1,jj}], 1] ]]];
Current best list for small 'locally $C_6$' graphs up to 20 vertices
Current best list for small 'locally $C_6$' graphs of 21 to 25 vertices (these have no defined names (yet) in Mathematica)
References