Questions on a New Proof of the Pythagorean Theorem

Question

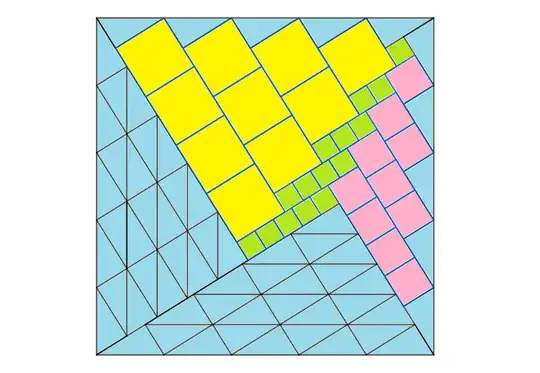
I am an elementary school teacher from South Korea who previously posted a question titled "a new Pythagorean proof here" I have gathered the answers from that question along with my own research to formulate a new set of questions (summarized in a paper I am working on here). I would like to ask for your opinion on the validity of these questions.

I am considering a problem that generalizes the dissection proof of the Pythagorean theorem: tiling an $nc \times nc$ square with a specific set of tiles for any natural number $n$. I have established what I believe to be a complete theoretical framework for this problem and would like to inquire about its validity. Problem Setup Goal: To perfectly tile an $nc \times nc$ square. Assumption: For a given right triangle $T_{a,b}$, its two legs, $a$ and $b$, are linearly independent over $\mathbb{Q}$ (i.e., $a/b$ is not a rational number). The length of the hypotenuse is $c = \sqrt{a^2 + b^2}$. Tile Set: The set of available tiles, $\mathcal{T}$, consists of the following four types:

$T_{a,b}$: A right triangle with base $a$ and height $b$. $S_a$: A square with side length $a$. $S_b$: A square with side length $b$. $S_{|a-b|}$: A square with side length $|a-b|$.

Core Question Is the following necessary and sufficient condition, along with its proof, valid? I propose that a tiling of the $nc \times nc$ square exists if and only if there is a non-negative integer solution $(N_a, N_b, N_T, k)$ that satisfies both of the following algebraic and combinatorial conditions. Here, $N_x$ represents the number of tiles of type $S_x$ or $T_x$, and specifically, $k = N_{|a-b|}$ is the number of "core tiles" $S_{|a-b|}$.

Algebraic Condition:

\begin{align}N_a + k &= n^2 \\ N_b + k &= n^2 \\ N_T &= 4k \end{align}

Combinatorial Condition:

$$k \geq n$$

I would appreciate a review of the rigor and completeness of the logical structure presented below to prove this proposition.

Proof Outline

1. Proof of Necessity ($\Rightarrow$)

Assumption: A valid tiling exists.

Derivation of the Algebraic Condition: We equate the total area of the $nc \times nc$ square, which is $n^2c^2 = n^2(a^2 + b^2)$, with the sum of the areas of all tiles used:

$$N_a a^2 + N_b b^2 + N_T \left(\frac{1}{2}ab\right) + k(a-b)^2$$

By expanding $(a-b)^2$ and rearranging, we get:

$$n^2a^2 + n^2b^2 = (N_a + k)a^2 + (N_b + k)b^2 + \left(\frac{N_T}{2} - 2k\right)ab$$

Since $a$ and $b$ are $\mathbb{Q}$-linearly independent, the terms $a^2$, $b^2$, and $ab$ are also linearly independent over $\mathbb{Q}$. By comparing the coefficients, the three algebraic equations are necessarily derived.

Derivation of the Combinatorial Condition ($k \geq n$): We consider the entire $nc \times nc$ square as an $n \times n$ grid of $c \times c$ cells. For structural integrity, each row and each column must contain at least one "core tile" ($S_{|a-b|}$). The minimum number of core tiles required to cover all $n$ rows and $n$ columns is $n$ (for example, by placing $n$ tiles along the main diagonal). Therefore, it must be that $k \geq n$.

2. Proof of Sufficiency ($\Leftarrow$)

Assumption: There exists an integer $k$ (where $n \leq k \leq n^2$) that satisfies both the algebraic and combinatorial conditions.

Constructive Proof using Mathematical Induction on $k$:

Base Case ($k = n$): I have demonstrated through a specific algorithm called "spiral dissection" that a geometric construction of the tiling is always possible for any natural number $n$ when $k = n$. This algorithm places the $n$ core tiles $S_{|a-b|}$ on the main diagonal and fills the remaining space with the other tiles.

Inductive Step ($m \rightarrow m+1$): Assume that for some integer $m$ such that $n \leq m < n^2$, a valid tiling $T_m$ with $k = m$ exists. Because $m < n^2$, the algebraic conditions imply $N_a = n^2 - m > 0$ and $N_b = n^2 - m > 0$. Therefore, the tiling $T_m$ must contain at least one $S_a$ tile and at least one $S_b$ tile.

A $c \times c$ area can be tiled by either a "simple module" consisting of $\{$one $S_a$, one $S_b\}$ or a "core module" consisting of $\{$one $S_{|a-b|}$, four $T_{a,b}\}$. Both modules have the same total area of $a^2 + b^2 = c^2$.

We find one "simple module" in the tiling $T_m$ and perform a local substitution with a "core module." This geometric transformation results in a new tiling $T_{m+1}$ that precisely satisfies the algebraic conditions for $k+1$:

• $k$ increases by 1 ($k \rightarrow k+1$).
• $N_a$ and $N_b$ decrease by 1.
• $N_T$ increases by 4.

Conclusion: Through this inductive process, we can construct the solutions for $k = n+1, n+2, \ldots, n^2$ starting from the base solution where $k = n$. Therefore, a tiling exists for every value of $k$ that satisfies the conditions.

Thus, could my overall approach—(1) specifying certain conditions as necessary and sufficient, and (2) proving their necessity through algebraic/combinatorial arguments and their sufficiency through constructive induction—be considered a valid theoretical framework for perfectly explaining the existence of solutions to this generalized Pythagorean proof problem?

Answer 1

I don't know what "structural integrity" means in this context or how it guarantees that there is a core tile in each row and column of the $n\times n$ grid of $c\times c$ cells. In fact, it seems that many tilings don't satisfy this property. For example:

I suspect it is true that in order to achieve the minimum number of core tiles in an $nc \times nc$ square $S$ you must have one in the exact center of each row and column of the $n \times n$ square grid within $S,$ but you have not proved that fact.

To prove that $k \geq n$ you might instead look at the number of triangles. In all tilings of an $nc \times nc$ square you have $n$ triangles along each edge of the square. Try showing that this is necessary by counting the edges of tiles of each kind that lie along one side of the large square. The entire side must be occupied by edges of tiles and no edges of tiles may overlap. The only edge lengths available are $a,$ $b,$ $\lvert a - b\rvert,$ and $c.$ Try to arrange it so these quantities are linearly independent over $\mathbb Q.$ Then the only way to tile $S$ is to have $n$ triangles along each edge of $S.$ Therefore $N_T \geq 4n,$ which implies that $k \geq n.$

To prove that there is a tiling for every solution of the equations and inequalities, you need to actually demonstrate your base case and prove that it always works for any $n.$ (I'm sure this is provable based on what we saw in your previous question and its answers, and maybe you have a proof that was too long to include in the question; I'm just saying the proof needs to exist somewhere.) Then, for the inductive step, I think it is necessary not just to say you can replace $a^2$ and $b^2$ squares with four triangles and a core tile; you need to show how each of these sets of shapes occupies the exact same region (the same set of points in the plane, not just two regions with the same area). From your previous results I'm sure you can do this, but it can't be done with the tiling above (for example), so it is necessary to actually show it.

I suspect that the easiest way to do this is actually to start with the $n \times n$ square grid inside $S,$ fill each cell with four triangles and a core tile in the same orientation, and identify $n^2 - n$ non-overlapping sets of four triangles and a core tile that each occupy the exact same region as an $a^2$ square and a $b^2$ square, thereby constructing your spiral dissection (or any dissection with exactly $n$ core tiles). Then any number of core tiles from $n$ to $n^2$ can be achieved by substituting the appropriate number of sets of tiles.