A new pythagorean proof

Question

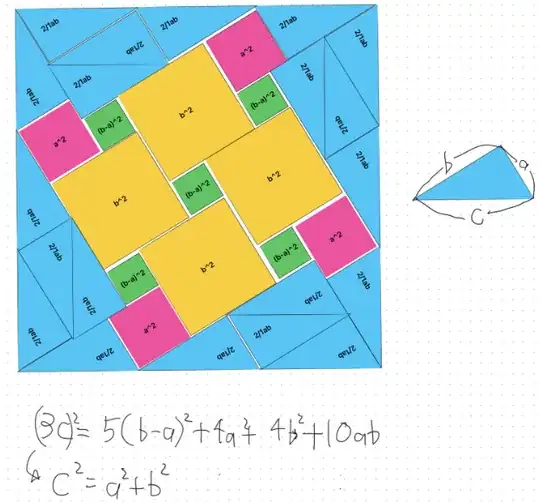
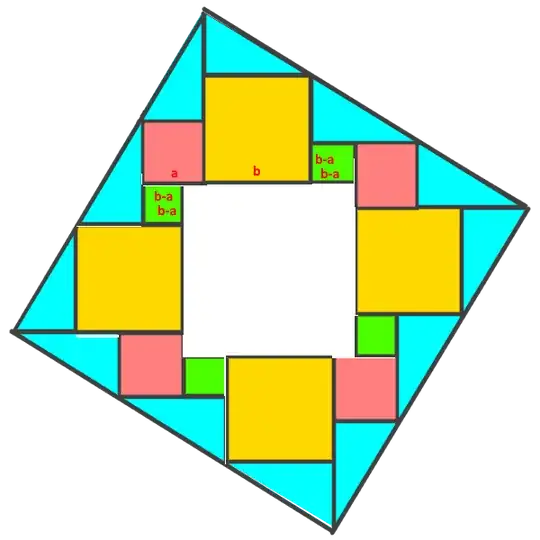
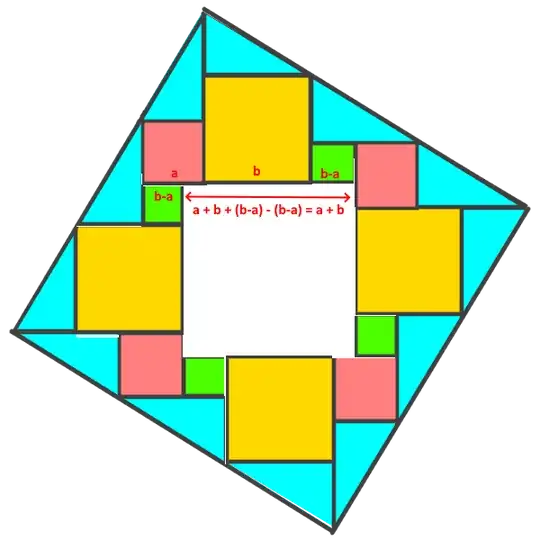
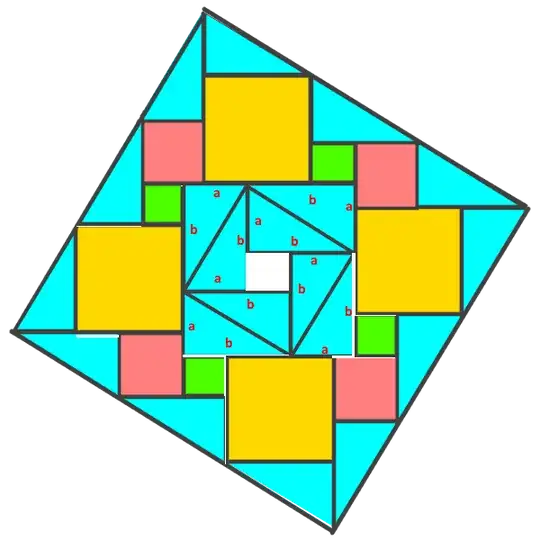
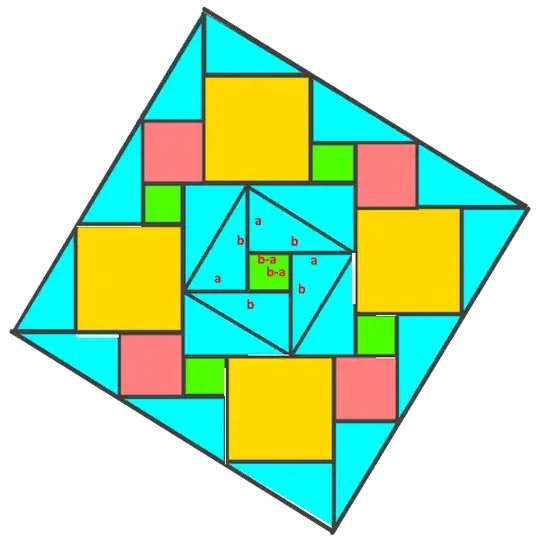
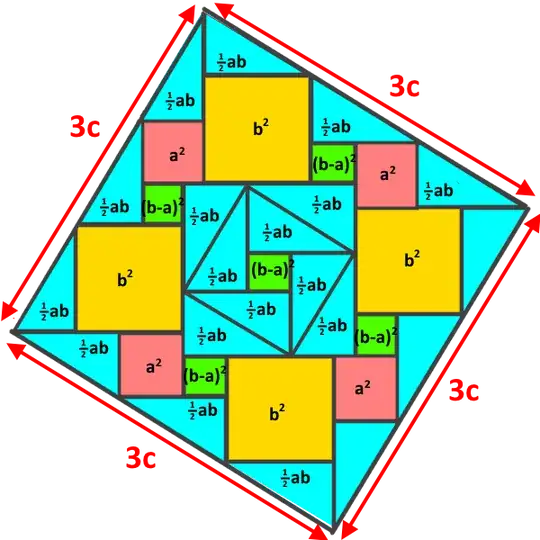
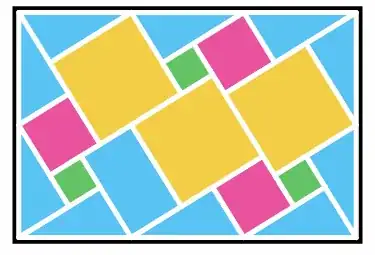
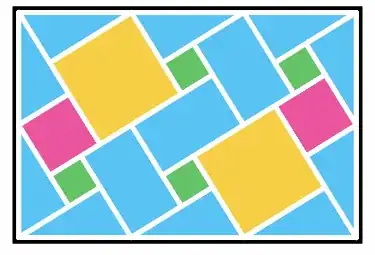
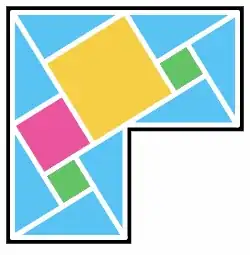
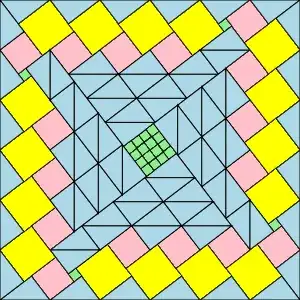
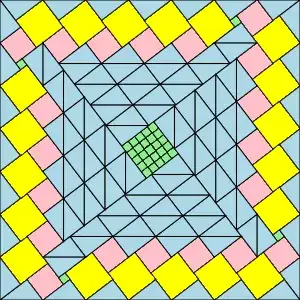
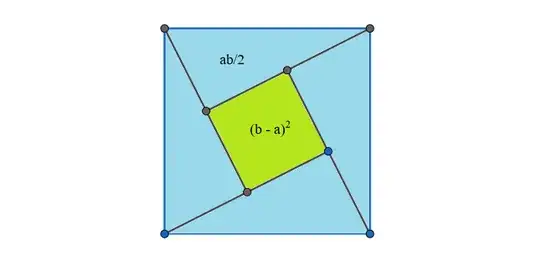
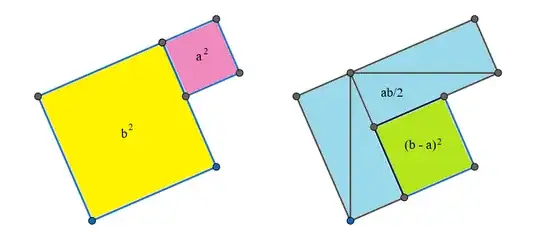
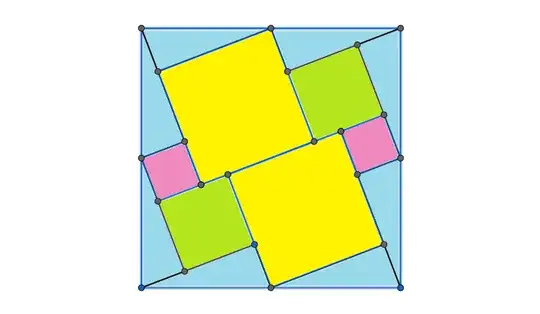
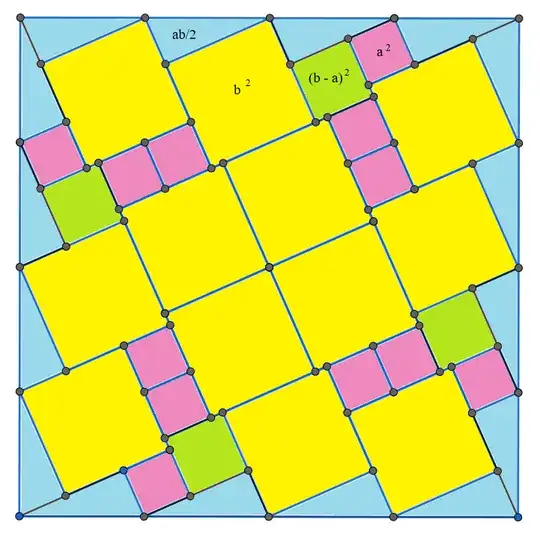
I am writing to you today because I believe I may have developed a new visual proof for the Pythagorean theorem. The proof is based on a geometric dissection method, equating the area of a larger composite square to the sum of its smaller constituent parts. I have attached an image file containing a diagram of the proof and the corresponding algebraic derivation.

The core of my derivation is that the area of the large square, which I represent as $(3c)^2$, is equal to the sum of the areas of the internal shapes: $5(b-a)^2 + 4a^2 + 4b^2 + 10ab$. This equation simplifies to the well-known Pythagorean identity, $c^2 = a^2 + b^2$. I am aware that there are hundreds of documented proofs of this theorem. However, I have not been able to find this specific dissection arrangement in my research.

Could you possibly spare a moment to review my work? I would be deeply grateful for your professional opinion on whether this proof is, to your knowledge, a novel discovery or a variation of a known proof. Thank you for your time and consideration.

*plus: I have recently been working on geometric proofs of the Pythagorean theorem. Following my recent development of a proof via a "$3c$ side" dissection, I have extended my research and believe I have established a unique dissection for a "$4c$ side" scenario.

I have consolidated my findings and was hoping you might be able to offer your expert assessment. Could you please let me know if you believe this proof is both valid and original? I would be very grateful for your feedback.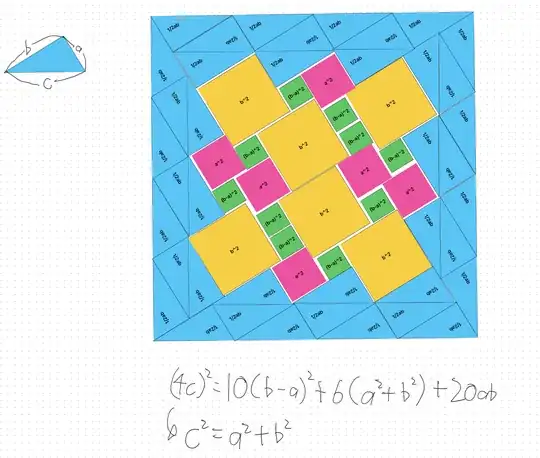

plus: I make $5c$ and new $3c$ too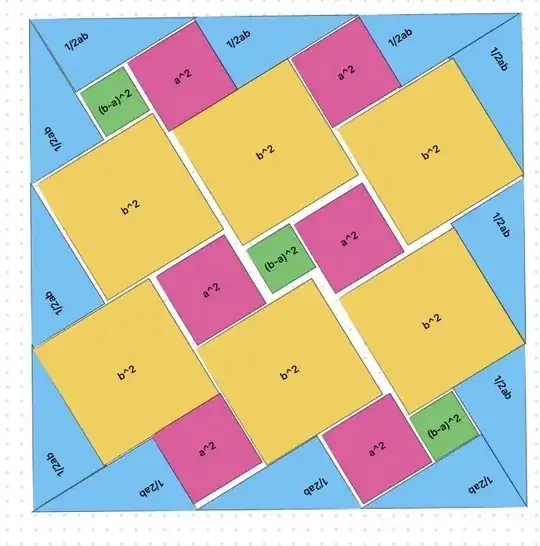 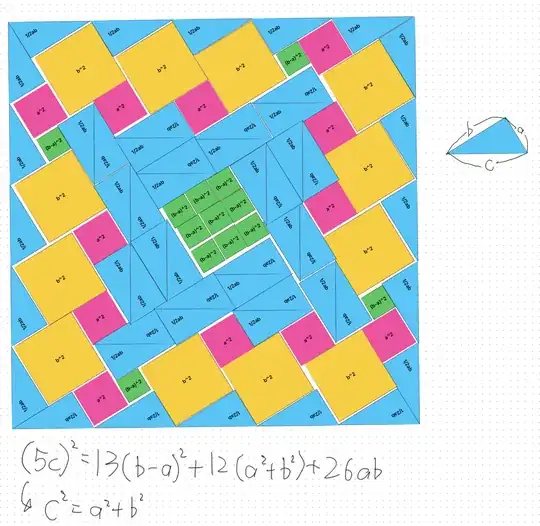Building on these findings, I am led to conjecture that an infinite series of such proofs might exist. It seems plausible that this method could be generalized for a hypotenuse corresponding to n units (where $n = 3, 4, 5, ...$), thus creating a potentially limitless set of proofs. As many of you in the comments have mentioned, the equation $$c^2(m + n)^2 = (a^2 + b^2)(m + n)^2 = (m^2+n^2)(b-a)^2+2mn(a^2+b^2)+2(m^2+n^2)ab$$ appears to be valid, suggesting that an infinite number of proofs could be constructed from it. My friend Ko and I have analyzed the proof methods, and we hypothesize that all the figures exhibit point symmetry.

P.S. I was excited to discover a general method for completing n x n composition patterns. It turns out the solution is to form a diagonal chain, as indicated by the black arrows in the diagram. I was genuinely surprised to have figured this out myself! This proof is conjectured to be special in that it requires the minimum number of triangles for an nc-tiling. This proof method I've developed operates based on the following equation(as @Blue mentioned):"

\begin{align}(nc)^2&=n(n-1)(a^2+b^2)+n(a-b)^2+4n\cdot\tfrac12ab\\&=n^2(a^2+b^2)+n\left(-(a^2+b^2)+(a^2+b^2-2ab)+2ab\right)\\&=n^2(a^2+b^2)\end{align}

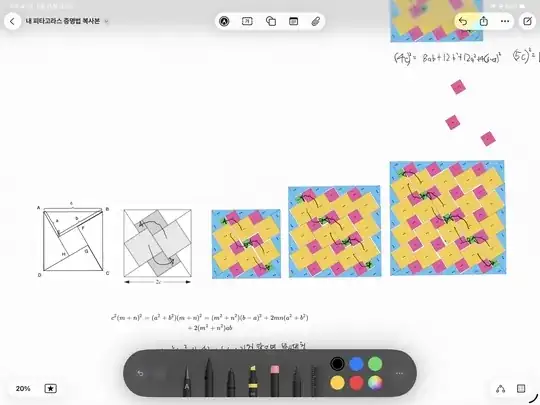
My conjecture is that when tiling a square with a side length of nc (where c is the hypotenuse), if n is a prime number, then this method is the unique way to create no more than the minimum of 4n triangles.

I have some research questions that I'm curious about but can't pursue myself, as I'm not a mathematician.

Regarding the aforementioned "$nc$ tiling," it has been proven that at least one tiling method exists where the number of triangles is minimized as '$n$' approaches infinity. However, I wonder:

Could we determine the number of tiling methods for a specific '$n$'? How many other tiling methods are there? As '$n$' approaches infinity, does the number of these methods also approach infinity? If so, what is the rate at which it approaches infinity? Based on my limited knowledge, it seems like these questions might be provable using series and analytical methods.

and I am an elementary school teacher in Korea, and as mathematics is not my primary field, I am unsure whether these findings warrant publication. If they do, I would greatly appreciate guidance on the process.

P.S. And this is my (and us) paper! click here

Answer 1

Too long (and animated) for a comment.

---

Well, this is just delightful.

One thing I like about this figure is that $a$ and $b$ aren't simply "short leg" and "long leg", swapping roles as the angles vary. Rather, they're functionally distinct: one leg has its corresponding square attached, the other doesn't. This gives the figure its chirality and the fact that, in the "extreme" instances (the apparent $3\times 3$ grid of squares), the visible $a$ and $b$ squares wind up in different spots: either (red) as corners of the grid or else (green) as neighbors of the center square.

---

I can't vouch for novelty of the figure, except to say that I personally don't recall seeing its like before. (Mind, my knowledge of proofs is far from encyclopedic ... and my memory is spotty. ;) That said, because it raises the questions "How can we decompose a $4c \times 4c$ square? a $5c \times 5c$ square? $nc \times nc$?", this seems like the kind of rabbit hole someone would have explored before. In that case, don't be discouraged: The fact that someone may have gotten to a result before you is merely (in the words of Steve Fisk) an "accident of time"; it doesn't diminish the fact that you got to it yourself. So, congratulations! :)

If this is novel, then you should see what you can do about those $4c \times 4c$, $5c \times 5c$, and $nc \times nc$ squares. :)

---

Addendum. Here's a representation of OP's variant tiling for an $nc\times nc$ square.

There are $n$ triangles along each side. The $a$-squares (also, the $b$-squares) are arranged in two triangular groups, with squares in each group offset by distance $c$ vertically and horizontally; the two groups are $n$ shy of completing an $n\times n$ grid. Finally, there are $n$ $|a-b|$-squares along the diagonal. Thus, we have $$\begin{align} (nc)^2 &\;=\; 4n\cdot\frac12ab \;+\; (n^2-n)\cdot (a^2+b^2) \;+\; n\cdot |a-b|^2 \\[4pt] &\;=\; n^2 (a^2+b^2) + n\left(\;2ab-(a^2+b^2)+(a^2+b^2-2ab)\;\right) \\[4pt] &\;=\; n^2(a^2+b^2) \end{align}$$

Some notes:

• The configuration trades the $4$-fold rotational symmetry of OP's original for $2$-fold rotational symmetry and straightforward extensibility.

• Also, this configuration lacks the original's "functionally distinct" $a$- and $b$-legs. That is, when the legs trade relative sizes, the figure effectively reflects over a diagonal of the enclosing square.

• In a comment, I suggested that the configuration may minimize the number of required triangles (and thus also the number of $|a-b|$-squares): $4n$ triangles (and $n$ of those squares). "Clearly" we need at least that many for the hypotenuses to account for the enclosing square's perimeter of $4nc$.

• I also wondered if the configuration was unique in its use of minimal triangles. It is not: @David K's answer includes a distinct $4c\times 4c$ configuration with $4\cdot 4$ triangles.

• In general, if there are $m\geq n$ squares of side $|a-b|$, then there must be $4m$ triangles (in order to cancel the $ab$ terms in the expression of area $(nc)^2=n^2(a^2+b^2)$ as the sum of integer multiples of $a^2$, $b^2$, $(a-b)^2$, and $\frac12ab$). This leaves $n^2-m$ copies each of the $a$-square and $b$-square.

• Typically, the previous point rules-out $4$-fold rotational symmetry (which would require that count to be divisible by $4$); the exceptions are when $(n,m)=(2p+r,4q+r)$, where $r\in\{0,1\}$. (For instance, in OP's original configuration with $(n,m)=(3,5)$; and @DavidK's $(n,m)=(4,4)$; and @SayanDutta's $(n,m)=(6,24)$ and $(7,29)$.) So, a "minimal triangle" configuration ($m=n$) with $4$-fold rotational symmetry must have $n=4p$ or $n=4p+1$.

Answer 2

Very nice!

I have taken the liberty to reorder parts of your drawing (apologies for the poor quality).

I think this reordering makes it much easier to calculate the side lengths of all the squares in the drawing (and to prove that they are indeed squares).

Addendum

I've been asked in the comments to elaborate a bit on my drawing.

1. Let's start with laying standard triangles (colored blue) along the edges like this:

2. Next add squares with side length a (colored magenta), and squares with side length b (colored yellow):

3. Now it is easy to see that next to the squares with side length b there is room for a small square with side length (b-a) (colored green)

4. Next it is important to notice that the sides of a group of magenta, yellow and green squares form a straight line. The sides of the white square have length (a + b + (b-a) - (b-a)) = (a+b).

5. So we can exactly place standard triangles inside the white square as shown, and place a set of standard triangles next to them to form rectangles.

6. This leaves a small square in the middle, with side length (b-a). For squares of this size we used the coler green before.

7. Now finally we can determine the areas of all elements in the drawing. OP has shown us how this leads to his pythagorean proof.

Answer 3

Bit too long for a comment, so here we go.

Aside from the first remark from Jean Marie, this looks perfectly fine.

I do have some questions though. First of all, visual proofs are great but also a bit dangerous. The main point that needs clarification is that the big square is indeed a square. The second thing you somehow need to verify is that it actually decomposes into this particular arrangement.

The technique you are using is similar to the standard visual proof by arranging the triangle into a square with sides of length $(a+b)$. See for example https://graphicmaths.com/gcse/trigonometry/pythagoras-proof/. Note that this link focuses on the justification more than the visual proof itself (and for good reasons).

Now I'm wondering why you are essentially using the same technique and arguments, but with a 'more complicated' arrangement. What line of reasoning brought you to this particular visual proof? (Also, I'm not attacking or criticizing your proof, don't take this as criticism! I'm genuinely curious how you came to this particular decomposition).

Answer 4

As others have noted already, the general form of these new proofs is, for parameters p,q: $$ \begin{aligned} (p+q)c^2 &= p(b-a)^2 + q(a^2+b^2) + 2pab \\ \implies c^2 &= a^2 + b^2 \end{aligned} $$

Restriction on p: Notice that the $2pab$ term includes the blue triangles which line the perimeter of every picture, each of which has area $ab/2$; this implies p can't be zero. More precisely, there are perimeter/c such triangles, implying p≥(perimeter/c)/4. There is no such restriction on $q$ (in particular, q may be zero).

In all the example pictures below,

• the red squares are $a^2$
• the yellow squares are $b^2$
• the green squares are $(b-a)^2$
• the blue rectangles are $ab$, and the blue triangles are $ab/2$

NOTE: although the animations are pretty, I find it impossible to study the animated pictures (and browsers provide no way to pause them), so I've provided both static and animated versions of all these examples.

Example: cut-the-knot proof #3

www.cut-the-knot.org/pythagoras #3
(p=1,q=0)
1c² = 1(b-a)² + 0(a²+b²) + 2ab

Example: cut-the-knot proof #116

www.cut-the-knot.org/pythagoras #116
(p=2,q=2)
(2c)² = 2(b-a)² + 2(a²+b²) + 4ab

Example: continuing the series of cut-the-knot proofs #3 and #116

Continuing the series q=p(p-1):

(p=3,q=6)
(3c)² = 3(b-a)² + 6(a²+b²) + 6ab

	[work in progress: animated gif was too big to upload]

(p=4,q=12)
(4c)² = 4(b-a)² + 12(a²+b²) + 8c

	[work in progress: animated gif was too big to upload]

(UPDATE 2025-06-20) Example: the other 3x3 with minimal blue

(p=3,q=6) (3c)² = 3(b-a)² + 6(a²+b²) + 6ab

Automated search found this alternative to the one shown above, using the same tiles.

Example: the new proof that started this all

Here's @mellowmelody355's example from the question:

(p=5,q=4)
(3c)² = 5(b-a)² + 4(a²+b²) + 10ab

A variant is also shown (not fundamentally different; it's formed by swapping the sizes and colors of a and b, and mirror-reversing the image):

		[work in progress: animated gif was too big to upload]

Example: 5x5 as suggested in a comment

Here's something that was suggested by @Intelligenti pauca in a comment:

(p=13,q=12)
(5c)² = 13(b-a)² + 12(a²+b²) + 26ab

Here are two possibilities of many, generated by hand. (Other people have given other solutions for this that generalize to larger sizes.) The black outline emphasizes the region where the two images differ.

	[work in progress: animated gif was too big to upload]
	[work in progress: animated gif was too big to upload]

Example: a non-square

The overall picture need not be square; here are some 3×2 rectangles:

(p=3,q=3)
(3×2)c² = 3(b-a)² + 3(a²+b²) + 6ab

(p=4,q=2)
(3×2)c² = 4(b-a)² + 2(a²+b²) + 8ab

Example: a non-rectangle (this is my favorite proof!)

The overall picture need not even be a rectangle:

(p=2,q=1)
3c² = 2(b-a)² + 1(a²+b²) + 4ab

It looks to me like this is the unique smallest example that has at least one of each tile color (or equivalently, q>0). Note that this can't be done in a 3x1 rectangle, even though it's the same size (since there isn't enough room for a yellow $b^2$ square there at all!)

(UPDATE) Example: a pentapythagoromino

@Blue suggested the name "pythagoromino" for pythagorean proofs on general polyominos, such as the previous example. Here's another.

Like the previous example, this can't be done on a rectangle.

(p=3,q=2)
5c² = 3(b-a)² + 2(a²+b²) + 6ab

(UPDATE) Example: a holyoctapythagoromino

We can call a pythagorean proof on a holyomino (polyomino with a hole) a "holypythagoromino". Here's one of order 8.

(p=4,q=4)
8c² = 4(b-a)² + 4(a²+b²) + 8ab

Example: all possible 2x2 proofs

Here are (I think) all possible ways of dissecting a 2x2 square, with all possible p,q:

(p=2,q=2)
(2c)²=2(b-a)²+2(a²+b²)+4ab (already shown earlier)

(p=3,q=1)
(2c)²=3(b-a)²+1(a²+b²)+6ab

(p=4,q=0)
(2c)²=4(b-a)²+0(a²+b²)+8ab

---

The images and animations were produced by constructing SVGs in javascript, and saved using html2canvas and gif.js.

Answer 5

Here's another family of $nc\times nc$ tilings that work. The pink, yellow, green squares have sides $a$, $b$, $|a - b|$ respectively; the blue right triangles have legs $a$, $b$.

While this does not have minimum number of triangles (like in OP's version), it does have rotational symmetry (unlike in OP's version). This corresponds to the equation $$4(n-2) (a^2 + b^2) + (n^2-4n+8) (a-b)^2 + 2(n^2-4n+8) ab = n^2 c^2$$ which corresponds to $m=2$ in your conjectured equation.

This is joint work with Satvik Saha.

$n = 6$	$n = 7$

Feel free to play with the animation here (p5js code here).

Notice that the $n=2$ case does not require any $a^2$ or $b^2$ squares (you can see this in the link by dragging the slider to the extreme left). And, the $n=1$ case is the original proof by picture (Proof #3 here).

This family of tilings admits a very large number of 'obvious' variantions by swapping tiles (for instance, each pink square forms a 'corridor' with blue rectangles within which it can be moved).

---

Lower bound on the number of triangles: Here's an argument (formalising the third bullet point of @Blue's answer) why a tiling of this nature must include at least $4n$ triangles: one can only use shapes with side lengths $a, b, c, (b - a)$ (assuming $b > a$) in order to produce the long side $nc$, hence a relationship of the form $$ k_1 a + k_2 b + k_3 (b - a) + k c =: k_1' a + k_2' b + kc = nc $$ for integers $k, k_i'$. But for a tiling to be truly general (in terms of the relative lengths of $a$ and $b$), the same relationship must hold with the parametrization $a = c\cos\theta, b = c\sin\theta$ for all $\theta \in (0, \pi/2)$. This reduces to something like $$ k_1'\cos\theta + k_2'\sin\theta + k = n, $$ which will force $k_1' = k_2' = 0$, $k = n$.

---

Admissible number of green squares: Borrowing the notation of Don's answer, this shows that a $(p, n^2 - p)$ tiling of the $nc\times nc$ square necessitates $p \geq n$ green squares. Indeed, every choice of $n \leq p \leq n^2$ admits a tiling: take your series of $(n, n^2 - n)$ solutions and successively apply the substitution of shapes from David's answer (note how nicely the yellow and red squares pair up!), increasing $p$ in steps of one all the way up to $n^2$. The final figure looks like $n^2$ copies of the $(1, 0)$ tiling arranged in a $n\times n$ grid; reversing this process gives another way of describing your series of solutions.

---

Feel free to check out my blog post on this topic.

Answer 6

This question proves that math really is fun.

If you reduce down to a square of side $c$ there seems to be only one useful way to dissect it:

Taking the legs of the triangles as $a$ and $b$ and the hypotenuse as $c,$ this shows that $c^2 = (b - a)^2 + 2ab = a^2 + b^2.$ This is listed as Proof #$3$ in the list of proofs of the Pythagorean Theorem at Cut the Knot.

One can also show that $c^2 = a^2 + b^2$ by rearranging the pieces of the square of side $c$ above into a shape that can be dissected into one square of side $a$ and one square of side $b$:

Now if you make a square with a side that is a multiple of $c$ you can tile it with copies of the square of side $c$ and then apply this substitution of shapes. For example, with a square of side $2c$ you can do the substitution twice to get this figure:

For a square of side $4c$ you can do the substitution $12$ times:

But your square of side $4c$ is different, showing that this kind of substitution is not the only way to dissect one of these squares.

In addition to this substitution it is also possible to dissect a square of side $kc$ into four triangles of legs $ka$ and $kb$ and a square of side $k\lvert b - a\rvert.$ Then you can dissect each triangle into $k^2$ congruent triangles and the square into $k^2$ congruent squares. Your square of side $5c$ can be derived from a square of side $3c$ in the center dissected in this way (so there are nine $(b - a)^2$ squares in the center) surrounded by sixteen squares of side $c$ dissected as in Proof #$3$, followed by some substitutions as shown above.

But the square of side $4c$ is more complex. There are other ways to rearrange a dissection; in particular, when some triangles and squares compose a shape with $180$-degree rotational symmetry you can rotate that shape by $180$ degrees to put the triangles and squares in different places. How you got the shape you have is a bit mysterious to me, however, which is part of the fun.

Could these dissections (and others like them) be a useful teaching device for young children? There are clearly endless variations possible as long as you can make a large enough square.